​Der Gini-Koeffizient ist ein statistisches Maß für Ungleichheit, das beschreibt, wie gleich oder ungleich Einkommen oder Vermögen in der Bevölkerung eines Landes verteilt sind. Er nimmt einen Wert zwischen 0 und 1 an, wobei ein höherer Gini-Koeffizient mit einer größeren Ungleichheit verbunden ist.

Obwohl sich die Wirtschaftswissenschaften häufig auf den Vergleich der Ressourcenzuweisung im Hinblick auf die Effizienz konzentrieren, ist die Verteilung von Einkommen und Vermögen in der Bevölkerung auch für politische Entscheidungsträger von großer Bedeutung. Länder mit einer extrem ungleichen Einkommens- oder Vermögensverteilung können anfälliger für soziale Unruhen und politische Instabilität sein (siehe auch Ungleichheit), und die Sorge um Fairness und Gerechtigkeit beeinflusst unsere Meinung über verschiedene politische Parteien und Umverteilungsmaßnahmen. Zur Messung der Ungleichheit und zum Vergleich der Ungleichheit zwischen verschiedenen Ländern oder Regionen verwenden Wirtschaftswissenschaftler häufig den Gini-Koeffizienten. Der Gini-Koeffizient ist ein statistisches Maß, das zum Vergleich verschiedener Verteilungen (von Einkommen oder Vermögen) verwendet wird. Er berücksichtigt, welcher Prozentsatz des Gesamteinkommens (oder -vermögens) in einem Land auf welchen Anteil der Bevölkerung des Landes entfällt. Ein Wert von Null (oder nahe Null) bedeutet, dass das Einkommen gleichmäßig auf die Mitglieder einer Gesellschaft verteilt ist. Dies wäre der Fall, wenn jeder genau das gleiche Einkommen hätte. Ein Gini-Koeffizient nahe bei 1 bedeutet, dass das Einkommen des Landes in den Händen sehr weniger Personen konzentriert ist. Stellt man sich beispielsweise ein Land mit 100 Personen vor, in dem eine Person alles besitzt und alle anderen kein Einkommen haben, so wäre der Gini-Koeffizient des Landes gleich 1.

Der Gini-Koeffizient wird grafisch durch Lorenz-Kurven dargestellt, wie in der folgenden Abbildung zu sehen ist. Auf der x-Achse ist der Anteil der Menschen, geordnet nach ihrem Einkommen, und auf der y-Achse der kumulative Anteil am Gesamteinkommen des Landes zu sehen. Die rote Linie entspricht einem Gini-Koeffizienten von 0, da das Einkommen gleichmäßig verteilt ist. Mit anderen Worten, die ärmsten 10 % der Bevölkerung haben das gleiche Einkommen wie die reichsten 10 %, was bedeutet, dass jeder Bürger den gleichen Anteil am Gesamteinkommen des Landes hat. In der nachstehenden Abbildung ents

pricht dies der roten Linie mit der Bezeichnung "perfekte Gleichheits Linie". Ein Gini-Koeffizient von 1 würde bedeuten, dass die reichste Person (oder sagen wir das reichste 1 %) in dem Land alles besitzt, während die übrigen 99 % kein Einkommen haben. Für die meisten Länder liegt der Gini-Koeffizient irgendwo zwischen 0 und 1. Dies entspricht einer Lorenzkurve, wie sie durch die blaue Linie in der Abbildung unten dargestellt ist.

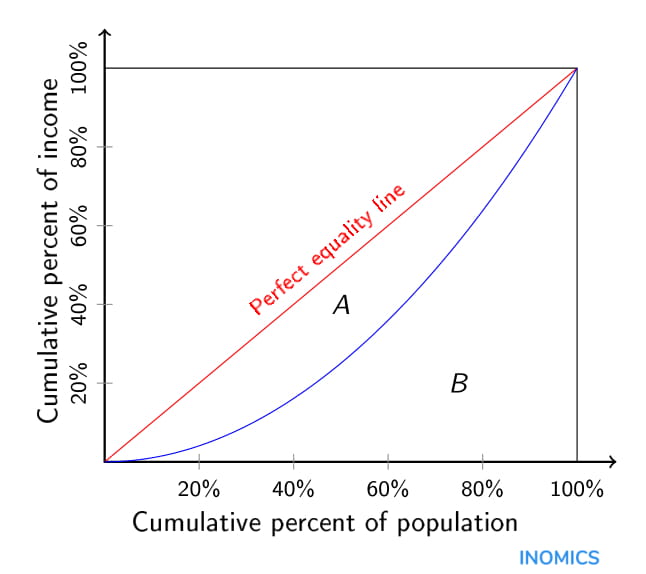
Lorenzkurven und damit Gini-Koeffizienten werden verwendet, um zwei (oder mehr) Einkommensverteilungen hinsichtlich ihrer Ungleichheit zu vergleichen. Eine Lorenz-Kurve, die näher an der roten Linie liegt, bedeutet einen niedrigeren Gini-Koeffizienten und damit ein geringeres Maß an Ungleichheit. Je weiter die Kurve von der roten Linie entfernt ist, desto ungleicher ist das Einkommen innerhalb der Gesellschaft verteilt. Mit Hilfe des Gini-Koeffizienten können wir die Ungleichheit in verschiedenen Ländern oder Regionen vergleichen, die Entwicklung der Einkommens- und Vermögensverteilung im Laufe der Zeit untersuchen oder die Auswirkungen bestimmter politischer Maßnahmen (z. B. die Auswirkungen einer Änderung der Einkommensteuer) auf die Einkommensverteilung analysieren.

Zur Berechnung des Gini-Koeffizienten können wir auch das Lorenz-Diagramm verwenden. Der Gini-Koeffizient, der der blauen Lorenzkurve in unserer Abbildung entspricht, kann wie folgt berechnet werden: \(Gini-index = \frac{A}{A+B}\). Die Fläche A ist die Fläche zwischen der perfekten Gleichheits Linie und der Lorenzkurve, während die Fläche B die Fläche zwischen der Lorenzkurve und den Achsen ist. Je größer B im Verhältnis zu A ist, desto geringer ist der Gini-Koeffizient und damit auch die Einkommensungleichheit in einem Land.

Jetzt wissen wir, was der Gini-Koeffizient misst und wie man ihn berechnet, aber interessanter ist es, die Gini-Koeffizienten über Länder und Zeit zu vergleichen, um zu sehen, welche Werte der Gini-Koeffizient annimmt und wie sich die Ungleichheit im Laufe der Zeit entwickelt hat. In der folgenden Tabelle sehen wir den Gini-Koeffizienten für fünf verschiedene Länder in zwei Jahren - 2000 und 2016.

Jedes der ausgewählten Länder hat einen Gini-Koeffizienten zwischen 0,27 und 0,53. Ein Gini-Koeffizient von 0,53 würde als hoch gelten und bedeuten, dass das Einkommen ziemlich ungleich verteilt ist, wie es in Mexiko der Fall ist. Der Gini-Koeffizient von etwa 0,28 für Norwegen bedeutet, dass das Einkommen in diesem Land gleichmäßiger verteilt ist (aber natürlich nicht vollkommen egalitär). Von den fünf betrachteten Ländern ist die Einkommensungleichheit in Mexiko am höchsten (gefolgt von den USA) und in Norwegen am niedrigsten.  In drei der fünf Länder (Deutschland, USA und Norwegen) ist der Gini-Koeffizient zwischen 2000 und 2016 gestiegen, während er in Mexiko gesunken ist. Die Daten stammen von der Weltbank, die auch Daten für viele weitere Länder und Jahre zur Verfügung stellt, wenn Sie einen genaueren Blick darauf werfen möchten.

Weitere Lektüre

Zu den bekanntesten Ökonomen, die sich mit Ungleichheit beschäftigen, gehören Thomas Piketty und Emmanuel Saez. In ihrem Papier "The evolution of top Incomes: A historical and international perspective" (veröffentlicht 2006 in der American Economic Review) präsentieren sie Erkenntnisse über die Entwicklung des Einkommens- und Vermögens Niveaus in einer Reihe von Ländern während des letzten Jahrhunderts. Eine der größten Herausforderungen beim Vergleich der Einkommensungleichheit zwischen den Ländern ist die mangelnde Homogenität der Daten und die fehlende Verfügbarkeit langfristiger Datenbanken. Eine der wichtigsten Erkenntnisse der Studie ist, dass im 20. Jahrhundert die Einkommensanteile der reichsten Menschen in der Gesellschaft während des Krieges und der Großen Depression entscheidend zurückgingen, was bedeutet, dass die Ungleichheit in diesen Zeiten abnahm.

Gut zu wissen

Der Gini-Koeffizient ist zwar ein nützliches und wichtiges Maß für die Ungleichheit, hat jedoch gewisse Einschränkungen, und Sie sollten sich auch andere Maße für die Ungleichheit ansehen, wenn Sie sich für die Untersuchung der Einkommens- (oder Vermögens-) Ungleichheit interessieren, um ein genaueres Bild zu erhalten. Andere häufig verwendete Maße sind der Theil-Index, der Hoover-Index, Perzentil Verhältnisse oder Einkommensanteile (Vergleich des mittleren Einkommens mit dem Medianeinkommen usw.).