Die Grenze der Produktionsmöglichkeiten (engl.: Production Possibilities Frontier) (PPF) ist ein Diagramm, das zur Beschreibung der Produktion einer Volkswirtschaft in der Makroökonomie oder der Produktionsentscheidungen eines Haushalts oder Unternehmens in der Mikroökonomie verwendet werden kann. Sie zeigt die möglichen Kombinationen von zwei (oder mehr) Produkten, die eine Volkswirtschaft herstellen kann, in einem einfachen Diagramm - daher der Name.

Die PPF wird häufig für zwei verschiedene Güter definiert, die mit den gleichen Inputs hergestellt werden; dies kann auf der vertikalen und horizontalen Achse eines Diagramms dargestellt werden. Je weiter man sich auf einer Achse bewegt, desto mehr von diesem Gut wird in der Wirtschaft produziert. Um den PPF zu erstellen, müssen Sie die Opportunitätskosten der Produktion jedes Gutes kennen. Mit anderen Worten: Sie müssen wissen, wie viele Einheiten des Gutes A Sie aufgeben müssen, um eine weitere Einheit des Gutes B auf allen Ebenen der Gesamtproduktion zu produzieren.

Um dies an einem einfachen Beispiel zu verdeutlichen, betrachten wir eine Wirtschaft, die Lebensmittel und Elektronik produziert. Nehmen wir weiter an, dass die einzigen Produktionsfaktoren in dieser Wirtschaft die Arbeitsstunden sind, die für die Herstellung der Güter erforderlich sind.

Die Produktion der Wirtschaft kann in der folgenden Tabelle dargestellt werden:

Wenn die Wirtschaft über eine Gesamtausstattung von 100 Arbeitsstunden verfügt, kann sie 1000 Einheiten Lebensmittel oder 500 Einheiten Elektronik produzieren, indem sie alle 100 Stunden für eines der beiden Güter aufwendet. Diese beiden Punkte sind die Schnittpunkte im PPF-Diagramm. Wenn wir die Nahrungsmittel auf der horizontalen Achse und die Elektronik auf der vertikalen Achse abbilden, dann sind der x-Achsenabschnitt 1000 und der y-Achsenabschnitt 500.

Nehmen wir nun an, dass die Anzahl der Arbeitsstunden, die zur Herstellung dieser Güter erforderlich sind, auf allen Produktionsniveaus konstant ist. Das heißt, unabhängig davon, ob wir 1 Einheit Lebensmittel oder 1000 Einheiten Lebensmittel herstellen, braucht es immer eine Arbeitsstunde, um 10 Einheiten Lebensmittel herzustellen. Das Gleiche gilt für Elektronik. Zusammengenommen ergeben diese Fakten den folgenden PPF:

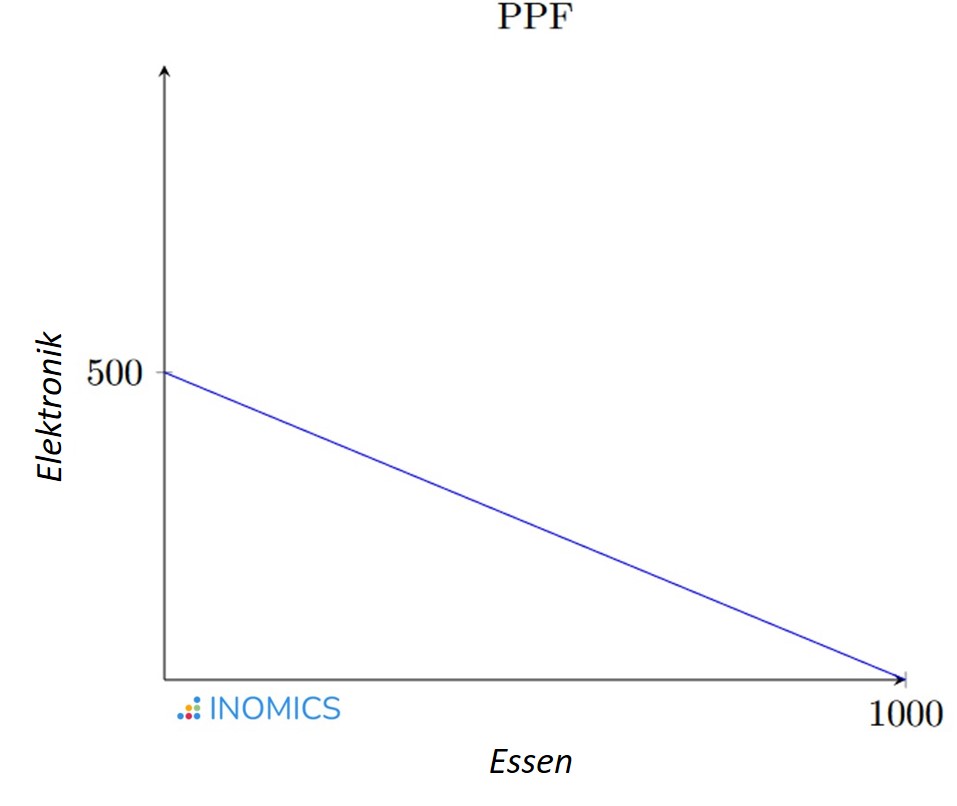
Ein nützlicher Aspekt der PPF ist, dass sie uns hilft, leicht zu erkennen, ob eine Volkswirtschaft ein pareto-effizientes Ergebnis erreicht hat. An jedem Punkt der dargestellten Linie setzt die Wirtschaft alle verfügbaren Arbeitsstunden ein, um eine bestimmte Mischung der beiden Güter zu produzieren. Dies ist im Sinne der wirtschaftlichen Produktivität effizient.

Aber jeder positive Punkt unter der Linie ist auch ein möglicher Produktmix. Das Problem dabei ist, dass sie ineffizient sind. Das liegt daran, dass die Wirtschaft einige ihrer verfügbaren Ressourcen ungenutzt lassen muss, um einen Punkt unter der Linie zu erreichen. In diesem Fall kann eine Pareto-Verbesserung erreicht werden, indem der Produktionsmix zu einem beliebigen Punkt auf der Linie verschoben wird, an dem alle verfügbaren Inputs genutzt werden.

Dies lässt sich leicht erkennen, wenn man an einem beliebigen Punkt unterhalb der Linie beginnt und sich vertikal bewegt, bis die Linie erreicht ist. In diesem Fall wird die gleiche Menge an Lebensmitteln (auf der horizontalen Achse) produziert, aber es wird mehr Elektronik produziert (vertikale Achse). Wir haben mehr Elektronik produziert, ohne Lebensmittel zu opfern, so dass die Wirtschaft grundsätzlich besser dasteht - eine Pareto-Verbesserung ist eingetreten.

Was bedeutet die Steigung des PPF? Denken Sie daran, dass die Steigung einer Linie ein Verhältnis ist, das die Änderungsrate der y-Variablen im Vergleich zur x-Variablen angibt. Erinnern Sie sich auch daran, dass wir davon ausgegangen sind, dass die Anzahl der Arbeitsstunden, die für die Produktion jedes Gutes eingesetzt werden, auf allen Produktionsniveaus konstant ist - mit anderen Worten, der Kompromiss zwischen den beiden Gütern ist immer derselbe. Das bedeutet, dass die Steigung der PPF an jedem Punkt die Opportunitätskosten zwischen den beiden Gütern ist!

Was passiert, wenn die Produktion in dieser Wirtschaft dem Gesetz des abnehmenden Ertrags unterliegt (ein häufigeres Szenario)? Das heißt, je mehr ein Gut produziert wird, desto mehr Arbeitsstunden werden für die Produktion der nächsten Einheit benötigt. Dies wäre der Fall, wenn die Produktionsfunktion so etwas wie eine Cobb-Douglas-Funktion wäre.

In diesem Fall ist das Diagramm gekrümmt, wie unten dargestellt:

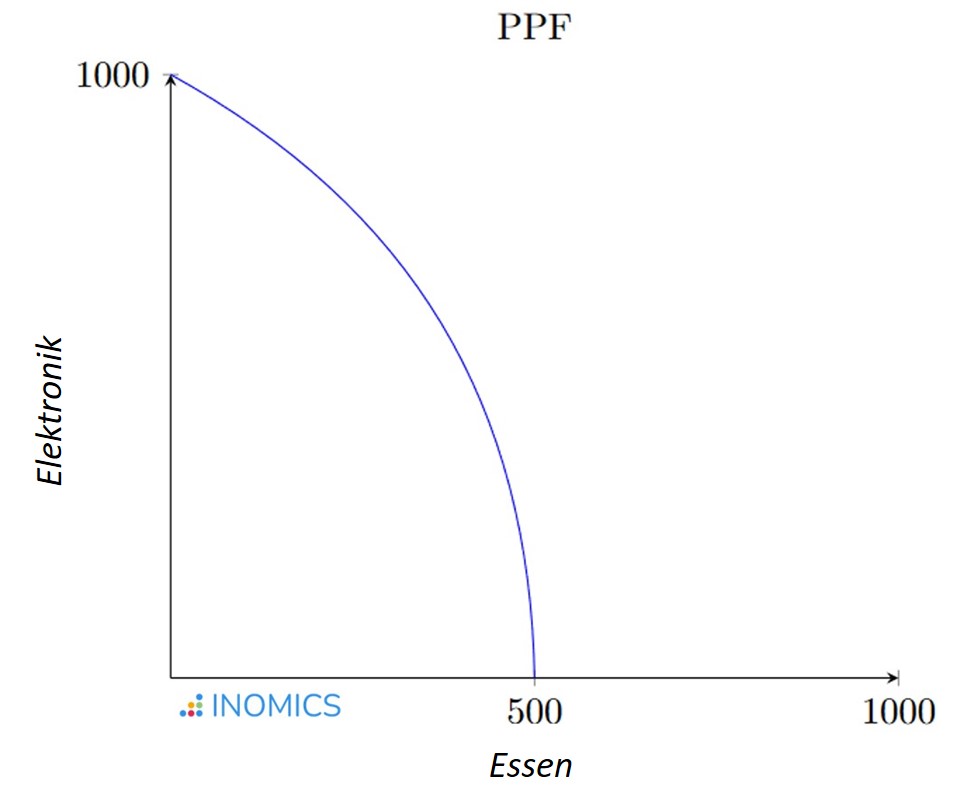
Die Opportunitätskosten für die Produktion eines der beiden Güter ändern sich, wenn man sich entlang des Diagramms bewegt. In der Nähe der y-Achse, wo wir hauptsächlich Elektronik produzieren, kostet es immer mehr Arbeitsstunden, die nächste Einheit Elektronik zu produzieren. Folglich geben wir immer mehr Einheiten von Nahrungsmitteln auf, um die nächste Einheit Elektronik zu produzieren. Wenn wir uns auf der Kurve nach unten bewegen, beginnen wir, mehr Nahrungsmittel und weniger Elektronik zu produzieren.

Wir können die Opportunitätskosten an jedem dieser Punkte ermitteln, indem wir die Ableitung der Funktion nehmen, um die Steigung zu erhalten. In diesem Fall sind die Opportunitätskosten für die Produktion von mehr Lebensmitteln umso höher, je näher wir uns der x-Achse nähern, und andersherum.

Größenvorteile lassen sich übrigens auch in der PPF darstellen. Skalenerträge bedeuten, dass die Opportunitätskosten für die Produktion eines Gutes sinken, wenn mehr von diesem Gut produziert wird. In diesem Fall hat das Diagramm wahrscheinlich eine nach innen gewölbte (konvexe) Form. Bleiben wir bei unserem Beispiel mit den Lebensmitteln und der Elektronik, so würde in diesem Fall eine weitere Bewegung entlang der x-Achse immer größere Mengen an Lebensmitteln und weniger an Elektronik produzieren. Die Opportunitätskosten für die Produktion einer weiteren Einheit Lebensmittel in Form von Elektronik würden jedoch abnehmen, je mehr Lebensmittel produziert werden.

Gut zu wissen

Das PPF definiert eindeutig den gesamten Produktmix, den eine bestimmte Volkswirtschaft produzieren kann. Wir haben bereits gesehen, dass jeder Punkt auf dieser Linie pareto-effizient ist. Aber für Volkswirtschaften, die mit anderen Volkswirtschaften Handel treiben, ist es tatsächlich möglich, dass ein Land an einem Punkt oberhalb seiner PPF konsumiert.

In dem Modell, das wir oben untersucht haben (eine theoretische Wirtschaft, die zwei Produkte in Autarkie produziert), ist dies nicht möglich. Jeder Punkt oberhalb des PPF stellt eine Produktionsmenge dar, die das Land nicht erreichen kann, weil es mehr Input (in diesem Fall Arbeitsstunden) benötigt, als verfügbar ist. Wenn wir zum Beispiel zu unserem linearen PPF-Beispiel zurückkehren, wäre es für das Land unmöglich, mehr als 1000 Einheiten Lebensmittel zu produzieren. Es kann 10 Einheiten Nahrungsmittel in einer Arbeitsstunde produzieren, und es hat 100 Arbeitsstunden zur Verfügung, so dass es maximal 1000 Einheiten Nahrungsmittel produzieren kann.

Wenn es um den Konsum geht, ist eine Handelswirtschaft aufgrund der Gewinne aus dem Handel, die der komparative Vorteil ermöglicht, nicht auf die gleiche Weise eingeschränkt. Wenn sich Länder auf die Produktion von Gütern spezialisieren, die sie relativ effizienter herstellen können, kann die Gesamtproduktion in der Weltwirtschaft tatsächlich höher sein, als wenn jedes Land nur für sich selbst produziert.  Wie das funktioniert, erfahren Sie in unserem Artikel über komparative Vorteil.