Economics Terms A-Z
Edgeworth Box
Read a summary or generate practice questions using the INOMICS AI tool
An Edgeworth box (named after Irish philosopher and economist Francis Ysidro Edgeworth, 1881) is a two-dimensional representation of a simple, closed economy consisting of two individuals and two items (or resources) that are finite in supply. Any feasible allocation of the items between the individuals is included as a dot in the box; the individuals’ preferences over the items are represented through indifference curves.
The advantage of depicting an economy in this way is to allow comparisons of different allocations and to determine their relative efficiency. Consider the following example of an economy with two individuals, Adam and Eve, and two items, dates and milk. The total number of dates in the economy is represented by the horizontal length of the box; the total amount of milk is measured by its vertical length. In the bottom-left corner \(o\), Adam has nothing while Eve owns/consumes all of the dates and milk. In the opposite top-right corner \(o'\), Adam possesses everything in the economy while Eve has nothing.
The indifference curves \(A_{1}\), \(A_{2}\) and \(A_{3}\) represent Adam’s preferences over dates and milk, with higher utility on \(A_{3}\) than \(A_{1}\); analogously, indifference curves \(E_{1}\), \(E_{2}\) and \(E_{3}\) represent Eve’s preferences over dates and milk, with higher utility on \(E_{3}\) than \(E_{1}\).
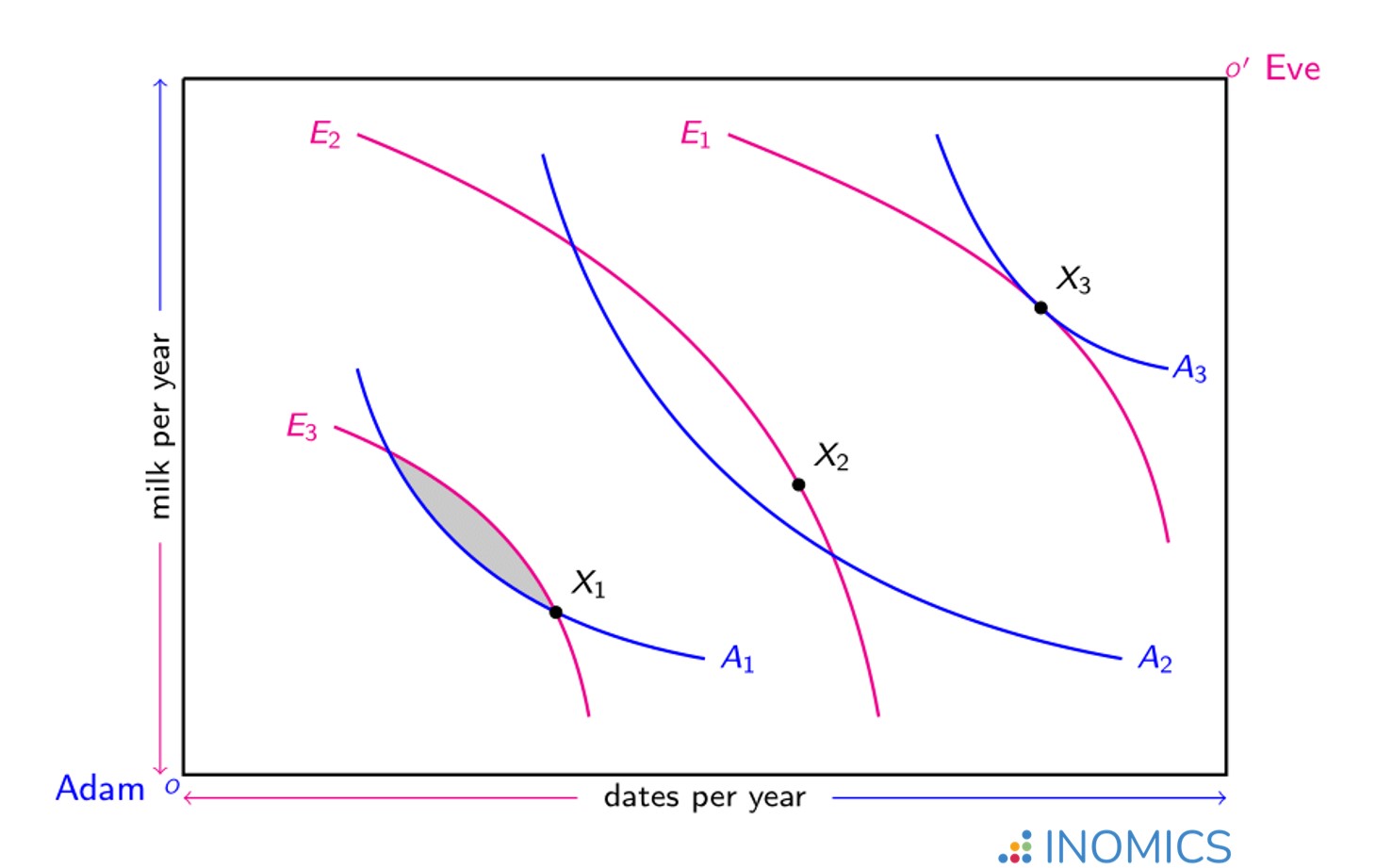
Figure 1: Edgeworth Box example
The points \(X_{1}\), \(X_{2}\) and \(X_{3}\) show three different allocations of dates and milk between Adam and Eve. At \(X_{1}\) Adam is on his indifference curve \(A_{1}\) while Eve is on her indifference curve \(E_{3}\). However this allocation is not Pareto-efficient because both Adam and Eve could be made better off (achieve higher utility) with another allocation anywhere within the grey shaded area bounded by indifference curves \(A_{1}\) and \(E_{3}\).
In contrast, the allocation at \(X_{3}\) where indifference curves \(A_{3}\) and \(E_{1}\) touch tangentially is Pareto-efficient because neither Adam nor Eve can achieve higher utility through a different allocation without reducing the other’s utility. Note however that at \(X_{3}\) Adam has significantly more dates and milk than Eve while the converse is true at \(X_{1}\). The fact that \(X_{3}\) is an efficient allocation says nothing about its fairness. Indeed, a point closer to the middle of the Edgeworth box, such as the allocation at \(X_{2}\), may be deemed more equitable than either \(X_{1}\) or \(X_{3}\) as the dates and milk are more evenly spread between Adam and Eve.
By reasoning similar to that at \(X_{1}\), the allocation at \(X_{2}\) is not Pareto-efficient; it can be improved upon without harming either individual in the economy. The set of Pareto-efficient allocations can be revealed in an Edgeworth box as a “contract curve” that runs between the origin corners (\(o\) and \(o'\)) through all of the points where indifference curves meet tangentially. This curve is depicted by the green line in Figure 2; every point on this line represents a Pareto efficient allocation where the indifference curves for both individuals are tangent to one another. Note that while each allocation on such a curve is efficient, it is not necessarily equitable!
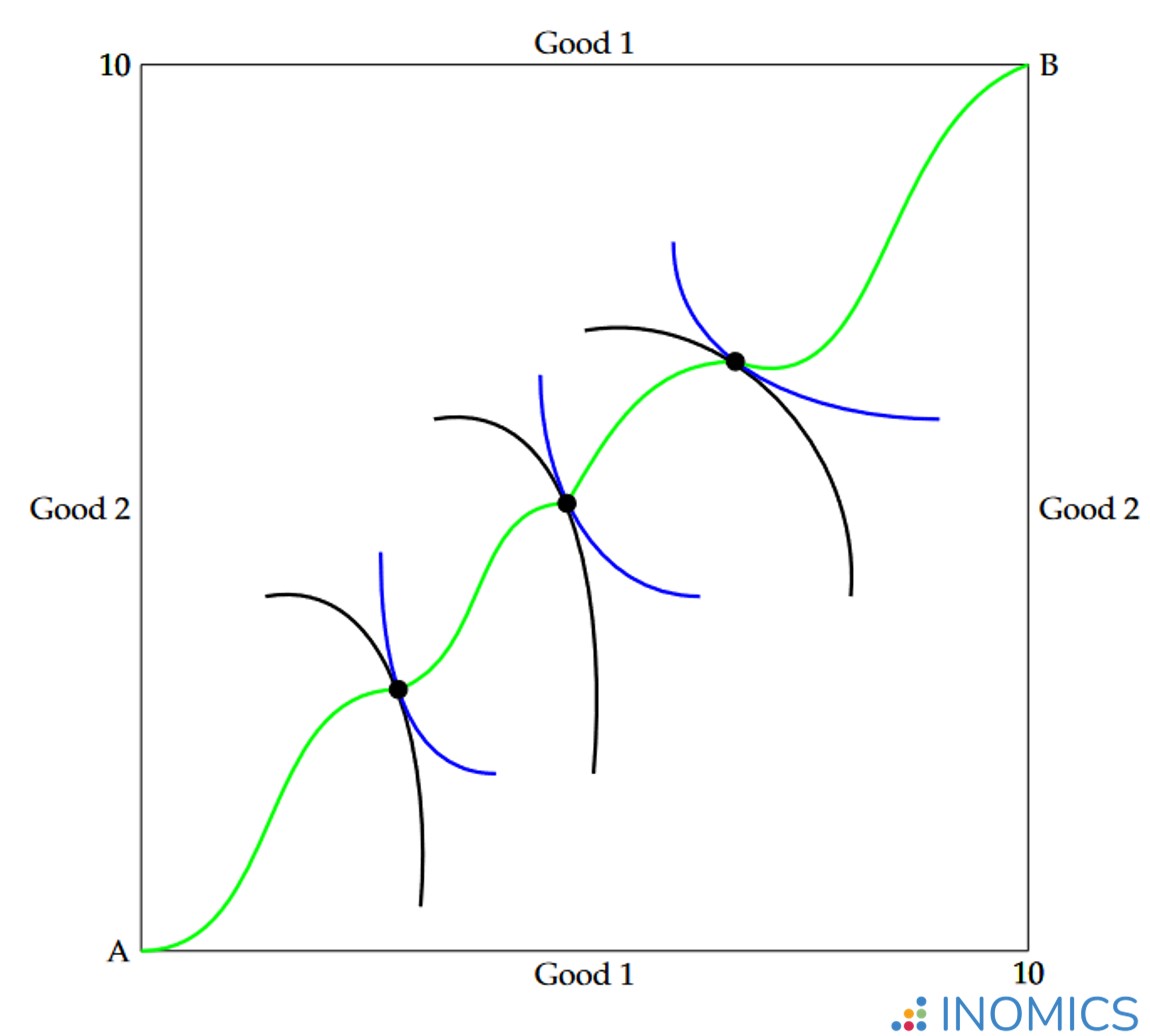
Figure 2: Contract curve depiction in an Edgeworth Box
Further reading:
The classic trade-off between efficiency and equity has long been a major point of contention in political economy. Koichi Tadenuma uses Edgeworth boxes to show how prioritising equity over efficiency can sometimes deliver more socially desirable outcomes, see his article, “Efficiency First or Equity First? Two Principles and Rationality of Social Choice” (Journal of Economic Theory, 2002).
Good to know:
Edgeworth boxes are a useful tool when considering the trade of two finite resources between two distinct economies. Utility in both economies can be shown to increase as trade allows the economies to achieve more efficient and equitable allocations of the resources than is possible in a state of autarky. Proponents of free trade may also argue that larger Edgeworth boxes can be achieved through exchange as the exploitation of each economy’s comparative advantage in production should lead to a greater overall availability of goods and services.
-
- PhD Program
- Posted 1 week ago
Graduate Program in Economics and Finance (GPEF) - Fully funded Ph.D. Positions
Starts 1 Sep at University of St.Gallen in Sankt Gallen, Switzerland
-
- Professional Training Course, Supplementary Course, Online Course
- (Online)
- Posted 5 days ago
Visualizing Geospatial Data In Stata: Spatial Maps In Stata - Live Online Course
Starts 10 Feb at TStat Training
-
- PhD Candidate Job
- Posted 3 weeks ago
PhD Candidate in Impact Evaluation of Welfare Programs
At NTNU: Norwegian University of Science and Technology in Trondheim, Norway














