Die Wohlfahrtsökonomie befasst sich mit der Frage, wie sich eine bestimmte Verteilung von Gütern und Ressourcen in einer Gesellschaft auf das wirtschaftliche Wohlergehen auswirkt. Sie zielt darauf ab, die öffentliche Politik zu einer Verteilung zu führen, die der Gesellschaft insgesamt zugute kommt. Als solche liefert sie die Instrumente, um verschiedene Ressourcen Zuweisungen zu vergleichen und sie unter dem Gesichtspunkt des sozialen Wohlergehens zu bewerten - oder laienhaft ausgedrückt, um zu beurteilen, wie "gerecht" diese Zuweisungen sind. Es gibt drei zentrale Konzepte, die in der Wohlfahrtsanalyse verwendet werden: Gesamtüberschuss, Allokationseffizienz und die soziale Wohlfahrtsfunktion.

Gesamtüberschüsse

In einem stilisierten Modell bezeichnet die Gesamt-Marktrente den Gesamtvorstand aller Teilnehmer an einem Markt. Sie ist die Summe der Konsumentenrente und der Produzentenrente, die als Nettogewinn für die Gesellschaft aus allen auf diesem Markt getätigten Geschäften (oder Transaktionen) verstanden werden kann.

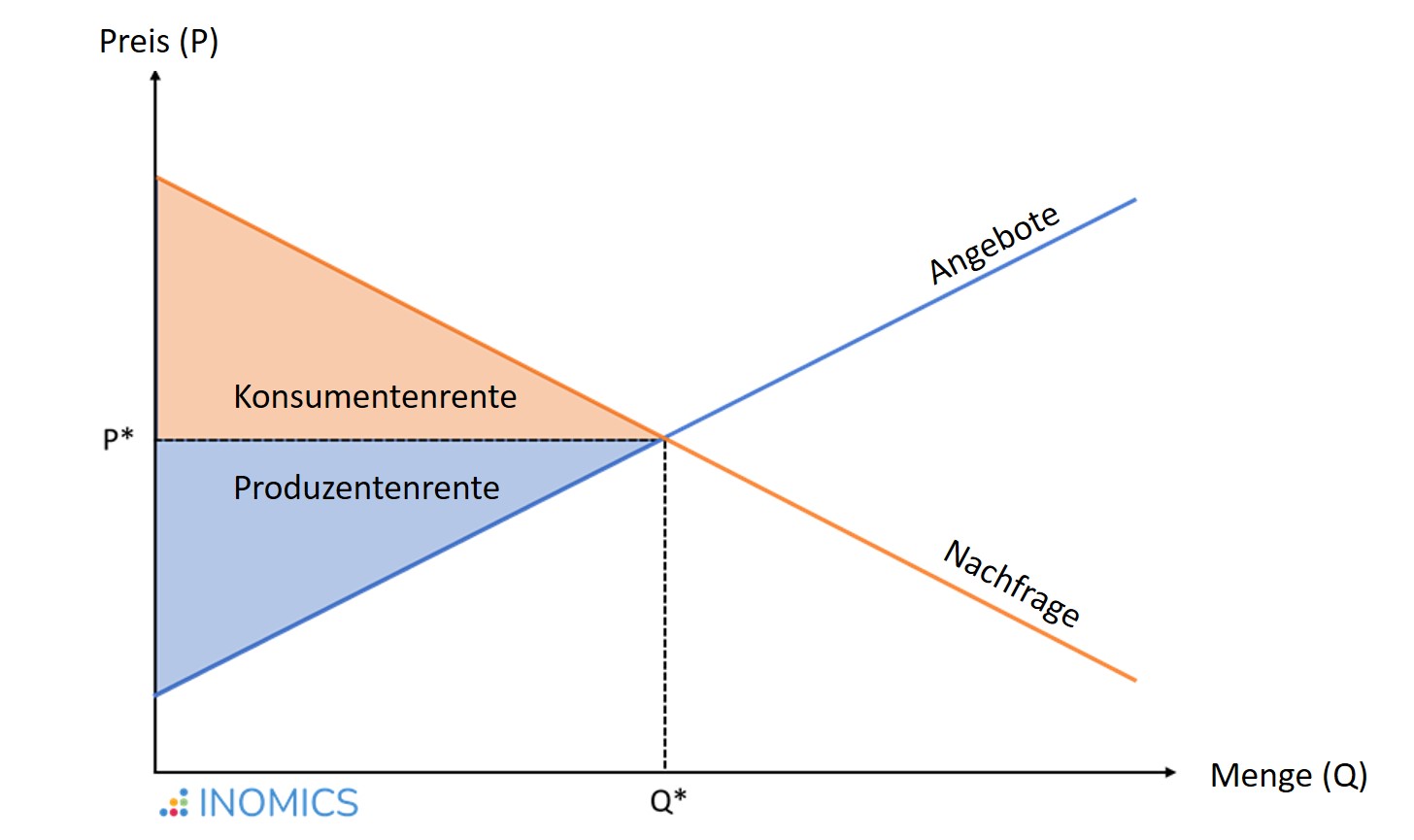
• Die Konsumentenrente einer Person ist die Differenz zwischen dem höchsten Preis, den sie für ein Produkt zu zahlen bereit ist, und dem Preis, den sie tatsächlich zahlt. Die Fläche unterhalb der Nachfragekurve und oberhalb des Marktpreises ist die gesamte Konsumentenrente, die sich aus der Summe aller Konsumenten auf dem Markt ergibt.
• Die Produzentenrente ist die Differenz zwischen dem niedrigsten Preis, den sie unter Berücksichtigung der Produktionskosten zu akzeptieren bereit wären, und dem Preis, zu dem das Produkt tatsächlich verkauft wird. Die Fläche oberhalb der Marktangebotskurve und unterhalb des Marktpreises ist die gesamte Produzentenrente, die sich aus der Summe aller Produzenten auf dem Markt ergibt.

Im Marktgleichgewicht, in dem das Angebot der Nachfrage entspricht (in der nachstehenden Abbildung mit P* und Q* bezeichnet), ist die Summe der Konsumenten- und Produzentenrente - und damit die Gesamtwohlfahrt - maximiert.

Im Falle von Marktineffizienzen, bei denen die auf dem Markt gehandelte Menge vom sozial effizienten Ergebnis abweicht, bleibt die soziale Wohlfahrt unter dem optimalen Ergebnis. Wenn z. B. Marktmacht es den Erzeugern ermöglicht, einen Preis P' > P* zu verlangen, reduziert sich die gehandelte Menge auf Q' < Q*.

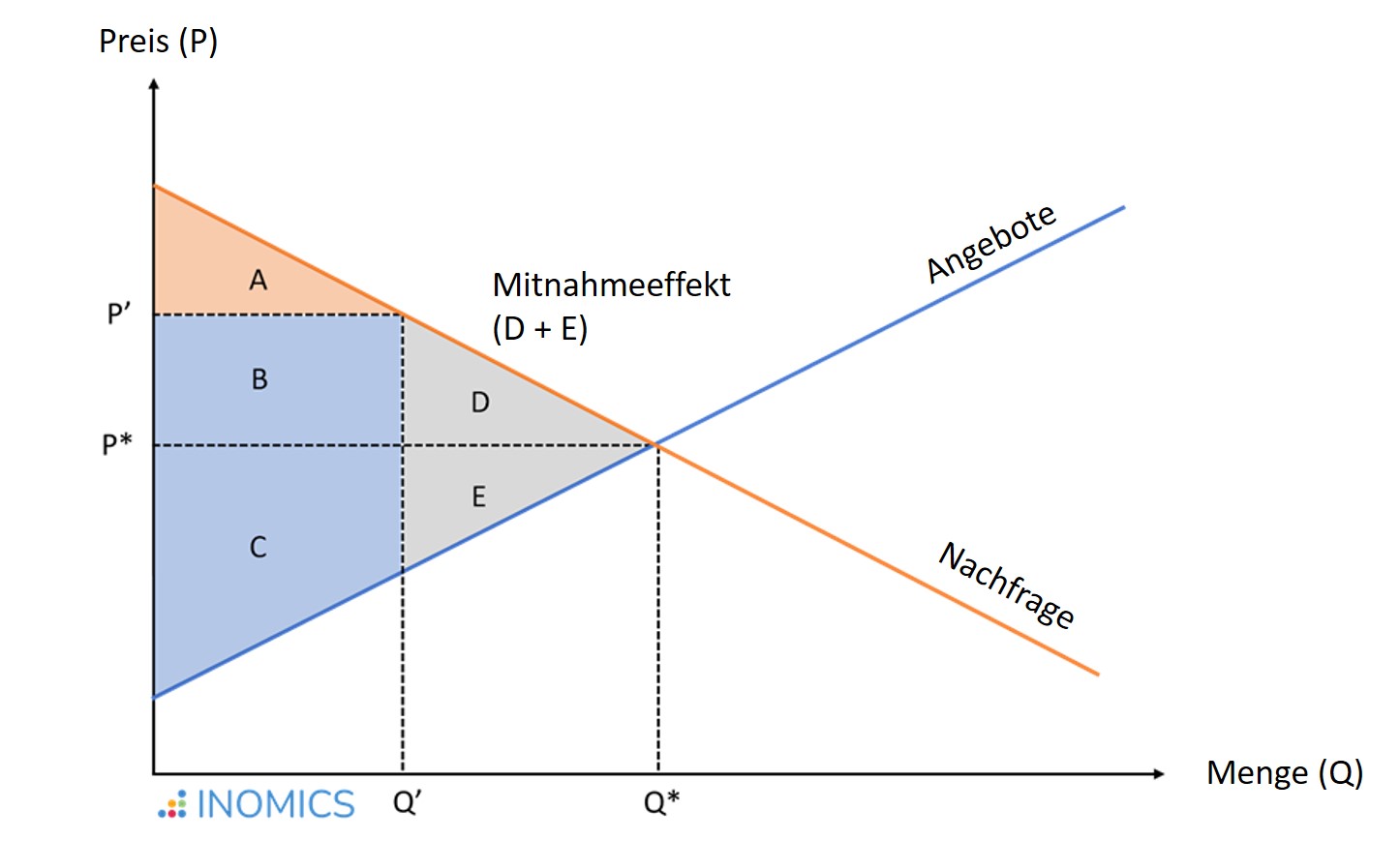
In dieser Situation ist die Konsumentenrente (CS) niedriger als im Gleichgewichtszustand:

\begin{equation*}
             CS' = A < CS^* = A + B + D,
    \end{equation*}

während die Produzentenrente (PS) höher ist als im Gleichgewicht:

\begin{equation*}
             PS' = B + C > PS^* = C + E.
    \end{equation*}

Während der Bereich B als Folge einer Preiserhöhung von den Verbrauchern auf die Erzeuger übertragen wird, spiegeln die Bereiche D + E den Wohlfahrtsverlust durch Mitnahmeeffekte wider, d. h. die Kosten, die der Gesellschaft durch die Ineffizienz des Marktes entstehen:

In Situationen, in denen Marktversagen zu einer ineffizienten Verteilung von Gütern und Dienstleistungen führt - wie in der oben dargestellten Situation - ist es möglich, eine alternative Verteilung zu finden, die mindestens eine Person besser stellt, ohne dass sich die anderen verschlechtern - und damit die soziale Wohlfahrt verbessert. In solchen Situationen kann ein staatliches Eingreifen potenziell das Wohlergehen aller verbessern.

Im obigen Beispiel könnte der Staat, wenn die Preise und Mengen auf die Gleichgewichtswerte (P*, Q*) festgelegt wären, eine pauschale Verbrauchsteuer in Höhe der Fläche B erheben. Anschließend könnte er diesen Betrag als pauschale Subvention an die Produzenten weitergeben, wodurch sich die Konsumentenrente um den Bereich D und die Produzentenrente um den Bereich E erhöhen würde.

Pareto-Effiziente Allokationen

Eine Zuteilung gilt als pareto-effizient (oder pareto-optimal), wenn kein weiterer Austausch möglich ist, durch den mindestens eine Person besser gestellt wird, ohne dass eine andere Person schlechter gestellt wird.

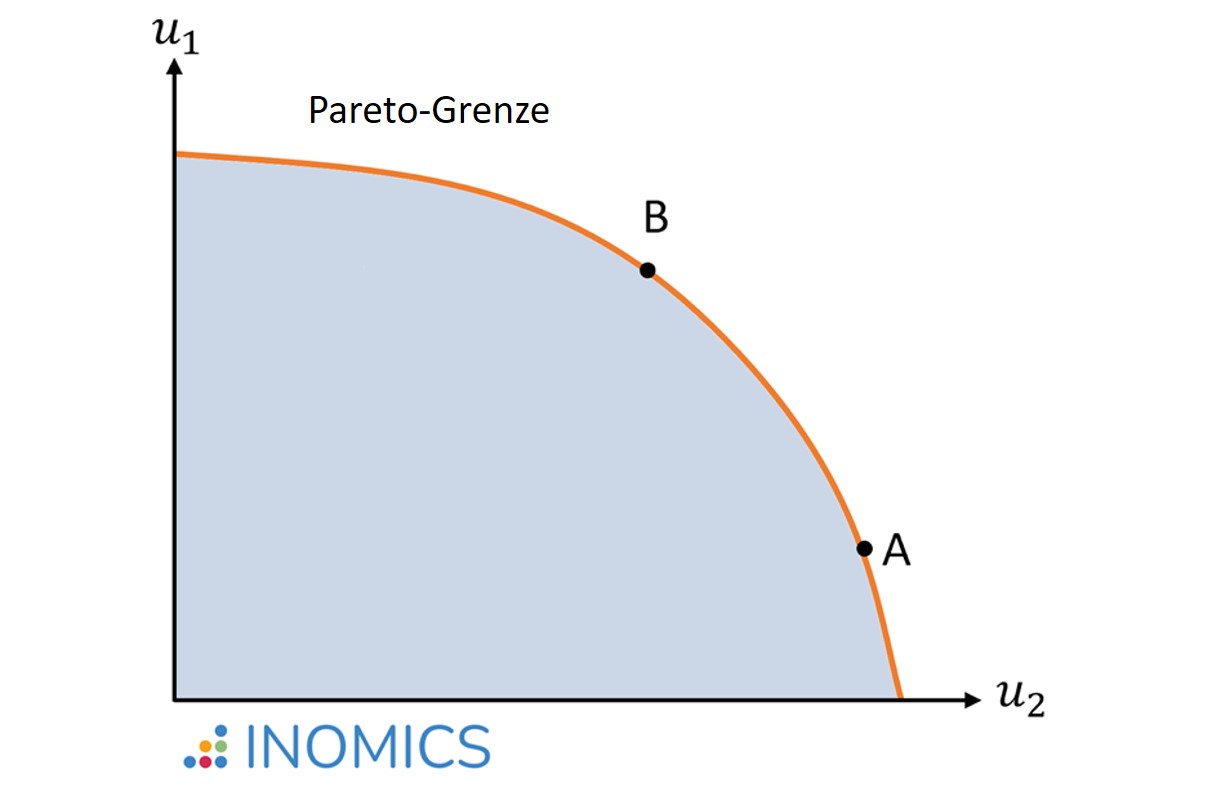
Das erste Theorem der Wohlfahrtsökonomie besagt, dass alle Wettbewerbs Gleichgewichte pareto-effizient sind, wenn es (1) keine externen Effekte, (2) vollkommenen Wettbewerb, (3) vollkommene Information (anstelle von asymmetrischer Information) und (4) vollkommen rationale Akteure gibt. Diese Gleichgewichte bilden die Pareto-Grenze (auch Pareto-Menge genannt). Dies ist in der folgenden Abbildung für eine Wirtschaft mit zwei Akteuren (1 und 2) dargestellt. Der blau schattierte Bereich stellt alle Kombinationen des Nutzens (u) dar, die zwar realisierbar, aber nicht effizient wären, da Ressourcen ungenutzt bleiben. Die orangefarbene Linie zeigt die Pareto-Grenze an, bei der alle Ressourcen genutzt werden und niemand besser gestellt werden kann, ohne dass jemand anderes schlechter gestellt wird.

Wichtig ist, dass die Pareto-Effizienz die Optimalität nur in einem begrenzten Sinne definiert, da sie keine "faire" Rangfolge zwischen verschiedenen Pareto-effizienten Verteilungen zulässt. So wird beispielsweise in der nachstehenden Abbildung nicht zwischen den Ergebnissen A und B unterschieden, obwohl Ergebnis A im Vergleich zu Ergebnis B erhebliche Ungleichheiten mit sich bringt.

Soziale Wohlfahrtsfunktion

Um verschiedene Ressourcen Zuweisungen nach ihrer sozialen Erwünschtheit einzustufen, verwenden Ökonomen in der Regel eine soziale Wohlfahrtsfunktion, W(u₁, u₂,...,u_H). Die soziale Wohlfahrtsfunktion ist bei individuellem Wohlstand nicht abnehmend, W'(u_H) > 0, und erreicht daher ein Maximum bei einem Pareto-Optimum.

Um ein konkretes Beispiel zu geben, stellen Sie sich eine Situation in einer Kindertagesstätte vor. Es gibt zwei Kinder, Lisa (L) und Tom (T), und zwei Spielzeuge, ein Buch (B) und ein Puzzle (P). Die Erzieherin überlegt, wie sie die Spielzeuge unter den Kindern aufteilen soll. Beide Kinder mögen beide Spielzeuge, aber Lisa mag Puzzles lieber als Bücher, während Tom beides gleichermaßen mag.

Nehmen wir an, dass Lisa einen Nutzen u_L(P) = 5 aus dem Lösen des Puzzles und einen Nutzen u_L(B) = 2 aus dem Lesen des Buches zieht. Tom zieht aus beiden Aktivitäten einen Nutzen u_T(P) = u_T(B) = 2. Unter der Annahme einer additiven Nutzen- und Soziale Wohlfahrtsfunktion wären die folgenden Allokationen und Nutzen Kombinationen machbar:

\begin{equation*}
     \text{Lisa: B,P; Tom:} \emptyset \quad \Rightarrow \quad
     W = u_L(P,B) + u_T(\emptyset) = (5+2) + 0 = 7 \\
     \text{Lisa: B; Tom: P} \quad \Rightarrow \quad
     W = u_L(B) + u_T(P) = 2 + 2 = 4 \\
     \text{Lisa: P; Tom: B} \quad \Rightarrow  \quad
     W = u_L(P) + u_T(B) = 5 + 2 = 7 \\
     \text{Lisa: } \emptyset; \text{Tom: B,P} \quad \Rightarrow \quad
     W = u_L(\emptyset) + u_T(P,B) = 0 + (2+2) = 4
    \end{equation*}

In diesem Fall wäre die zweite Zuteilung nicht effizient. Durch den Tausch der Spielzeuge kann eine Pareto-Verbesserung erreicht werden: Wenn Tom das Puzzle an Lisa und Lisa das Buch an Tom gibt, erhöht sich Lisas Nutzen, während Toms Nutzen gleich bleibt.

Auch die vierte Aufteilung lässt Raum für Verbesserungen. Würde Tom das Rätsel an Lisa geben und nur das Buch behalten, würde der gesamte Wohlstand steigen. Toms Nutzen würde jedoch sinken, wenn er nicht irgendwie entschädigt würde. Lisa könnte Tom für die Abgabe des Rätsels entschädigen, da ihr Wohlfahrtsgewinn durch den Tausch größer ist als sein Wohlfahrtsverlust.

Lisa könnte Tom zum Beispiel anbieten, ihm das Buch vorzulesen, wenn er ihr das Rätsel gibt. Wenn diese Kompensation (C) für Lisa Nutzen Kosten von u_L(C) <  u_L(P) und für Tom einen Nutzengewinn von  u_T(C) ≥  u_T(P) mit sich bringt, dann wird eine Pareto-Verbesserung erreicht, indem das Rätsel gegen eine Kompensation "getauscht" wird. Wenn, sagen wir, das Vorlesen des Buches für Tom Nutzen Kosten von uT(C) = 2 für Lisa und einen Nutzengewinn von  u_T(C) = 2 für Tom mit sich bringt, wäre die Gesamtwohlfahrt nach dem Tausch W =  u_L(P) -  u_L(C) +  u_T(B) +  u_T(C) = (5-2) + (2+2) = 7. Auf einem Markt mit Geld besteht die offensichtliche Lösung darin, dass die erwachsene Lisa dem erwachsenen Tom das Rätsel für einen Betrag  u_T(P) ≤ x ≤  u_L(P) bezahlt.

Sowohl die erste als auch die dritte Zuteilung in der obigen Beispielliste sind Pareto-effizient. Kein Kind kann besser gestellt werden, ohne dass das andere schlechter gestellt wird. Wie diese Zuteilungen eingestuft werden, hängt jedoch von der funktionalen Form der sozialen Wohlfahrtsfunktion ab. Bislang haben wir eine additive Struktur angenommen: Lisas und Toms Nutzen sind perfekte Substitute.

Wir könnten auch eine multiplikative Struktur annehmen, in diesem Fall sind Lisas und Toms Nutzen Ergänzungen, und Ungleichheit wird bestraft. Dies ist typischerweise im realen Leben der Fall, da der Grenznutzen von fast allem abnimmt; eine ärmere Person schätzt einen zusätzlichen Euro mehr als eine reiche Person. In diesem Fall maximiert die dritte Allokation die soziale Wohlfahrt in der Kindertagesstätte:

\begin{equation*}
     \text{Lisa: B,P; Tom:} \emptyset \quad \Rightarrow \quad
     W = u_L(P,B) \times u_T(\emptyset) = (5+2) \times 0 = 0
    \end{equation*}
\begin{equation*}
     \text{Lisa: B; Tom: P} \quad \Rightarrow \quad
     W = u_L(B) \times u_T(P) = 2 \times 2 = 4
    \end{equation*}
\begin{equation*}
     \text{Lisa: P; Tom: B} \quad \Rightarrow  \quad
     W = u_L(P) \times u_T(B) = 5 \times 2 = 10
    \end{equation*}
\begin{equation*}
     \text{Lisa: } \emptyset; \text{Tom: B,P} \quad \Rightarrow \quad
     W = u_L(\emptyset) \times u_T(P,B) = 0 \times (2+2) = 0
    \end{equation*}

Nach dem zweiten Wohlfahrtstheorem kann jedes Pareto-Optimum durch ein Wettbewerbsgleichgewicht erreicht werden, wenn pauschale Steuern und Transfers zur Verfügung stehen, um die individuellen Ausstattungen zu verschieben. Wenn beispielsweise die anfänglichen Ausstattungen in der obigen Abbildung zu Punkt A führen und unsere soziale Wohlfahrtsfunktion Punkt B bevorzugt, können wir eine Pauschalsteuer für Individuum 2 erheben und sie an Individuum 1 weitergeben, um diese Verschiebung im resultierenden Gleichgewicht zu bewirken.

Im Beispiel der Kindertagesstätte könnte die Erzieherin, wenn Lisa sich für das Buch und das Puzzle entscheiden würde (Zuteilung 1), eingreifen und Lisa das Buch wegnehmen, um es Tom zu geben (Zuteilung 2), und so zwischen zwei Pareto-effizienten Zuteilungen wechseln, um die sozial optimale zu erreichen.

Leider sind die Möglichkeiten des Staates, Pauschalsteuern zur Verbesserung der Ressourcenverteilung in einer Gesellschaft einzusetzen, in der Praxis begrenzt. Bei einer Pauschalsteuer handelt es sich um einen festen Betrag, den der Einzelne auf der Grundlage seiner Eigenschaften und unabhängig von seinen Entscheidungen zahlt. Stellen Sie sich zum Beispiel eine Volkswirtschaft mit 10 Personen vor, von denen 5 ein Anfangsvermögen von 100 € haben, während die anderen 5 ein Anfangsvermögen von 0 € haben. Nehmen wir an, dass die soziale Wohlfahrt maximiert würde, wenn diejenigen, die 100 € haben, 50 € an diejenigen zahlen würden, die nichts haben.

Diese Umverteilung kann jedoch die Anreize des Einzelnen, künftigen Wohlstand zu schaffen, zunichte machen, wenn alle Gewinne unabhängig vom Arbeitseinsatz des Einzelnen gleichmäßig verteilt werden. Außerdem sind die Informationen über das ursprüngliche Vermögen für den Staat möglicherweise nicht direkt einsehbar.

Gut zu wissen

In der Praxis werden staatliche Entscheidungen selten in Situationen getroffen, in denen Pareto-Verbesserungen möglich sind. Meistens muss die Regierung einen Kompromiss zwischen den Bedürfnissen und Interessen verschiedener Gruppen eingehen, und die Auswirkungen verschiedener Entscheidungen auf die Gesamtwohlfahrt sind nicht immer klar.

Nehmen wir zum Beispiel an, die Regierung erwägt den Bau einer neuen Autobahn. Diejenigen, die die Autobahn nutzen wollen, um schneller zur Arbeit zu gelangen oder ihre Produkte schneller zu transportieren, sind bereit, eine Nutzungsgebühr zu zahlen, die die Kosten für Bau und Instandhaltung deckt. Auf den ersten Blick mag der Bau dieser Autobahn eine Pareto-Verbesserung darstellen: Einige Personen werden dadurch eindeutig besser gestellt.

Es wird aber höchstwahrscheinlich auch Menschen geben, die durch die Autobahn beeinträchtigt werden. Verkehrsbehinderungen und Staus können während der Bauphase negative Nebeneffekte haben, und ganze Stadtteile können durch den Lärm der Autobahn beeinträchtigt werden. In diesem Fall kann die Regierung die negativen Auswirkungen verringern (z. B. durch den Bau eines Lärmschutzwalls) und/oder die Betroffenen entschädigen, die weiterhin negativ betroffen sind.

Der Ausgleich widerstreitender Interessen wird in Zeiten großer Krisen noch schwieriger, wie die COVID-19-Pandemie gezeigt hat. Strategien zur Bewältigung von Risiken für die öffentliche Gesundheit bergen selbst Risiken. Der Gesundheitssektor ist in Gebieten, in denen keine Pandemie herrscht, Risiken ausgesetzt, da Ressourcen für die Behandlung und Bekämpfung von COVID-19 abgezweigt werden. In der Zwischenzeit sind Unternehmen, potenzielle Opfer häuslicher Gewalt und die Bildung von Kindern allesamt Bereiche, in denen Pandemie-Reaktionsprotokolle eine Situation verkomplizieren und einige Gruppen während der Erholungsphase einer Pandemie relativ schlechter stellen können als der Durchschnitt.

Expertenrat kann dazu beitragen, einige dieser Kompromisse zu klären, aber der Vergleich der einzelnen Gewinne und Verluste, die sich aus jeder politischen Option ergeben, und die Suche nach der sozial optimalen Lösung sind nicht so einfach, wie die oben vorgestellten einfachen Beispiele vermuten lassen.