La economía del bienestar estudia el efecto de una determinada asignación de bienes y recursos en una sociedad sobre el bienestar económico. Su objetivo es tratar de guiar las políticas públicas hacia una asignación que beneficie a la sociedad en general. Como tal, proporciona las herramientas necesarias para comparar distintas asignaciones de los recursos y evaluarlas desde una perspectiva asociada al bienestar social – o en términos sencillos, para juzgar qué tan "justas" son esas asignaciones. En el análisis del bienestar se utilizan tres conceptos básicos: excedente total, eficiencia distributiva, y la función del bienestar social. 

Excedente Total

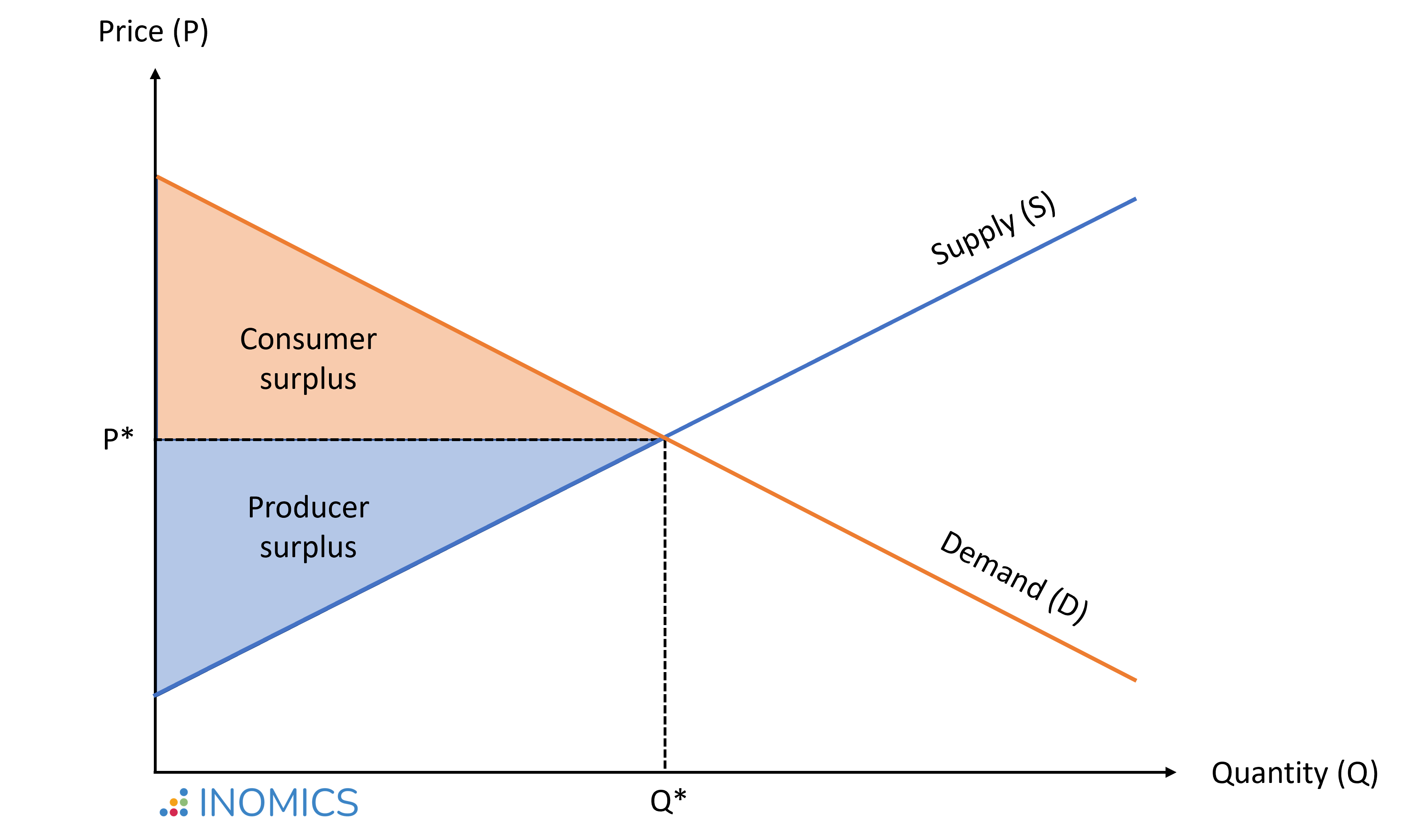
En un modelo estilizado, el excedente total del mercado indica el bienestar total de todos los participantes de un mercado. Es el resultado de la suma del excedente del consumidor y el excedente del productor, que se puede interpretar como el beneficio neto de una sociedad derivado de todas las operaciones (o transacciones) que se realizan en ese mercado. 

• El excedente del consumidor es la diferencia entre el mayor precio que los individuos estén dispuestos a pagar por un producto y el precio que acaban pagando. El área inferior a la curva de la demanda y superior al precio de mercado es el excedente total del consumidor, sumado para todos los consumidores en el mercado. 
• El excedente del productor es la diferencia entre el menor precio que las empresas estarían dispuestas a aceptar, considerando los costes de producción, y el precio por el cual se acaba vendiendo el producto. El área superior a la curva de la oferta del mercado e inferior al precio de mercado es el excedente total del productor, sumado para todos los productores en el mercado. 

En el equilibrio de mercado, donde la oferta es igual a la demanda (designado por P* y Q* en el gráfico inferior), la suma del excedente del consumidor y del productor – y por lo tanto el bienestar total – está maximizada.

In case of market inefficiencies, where the quantity traded on the market diverges from the socially efficient outcome, social welfare remains below the optimal outcome. For example, if market power allows producers to charge a price P' > P*, this reduces the quantity traded to Q' < Q*.

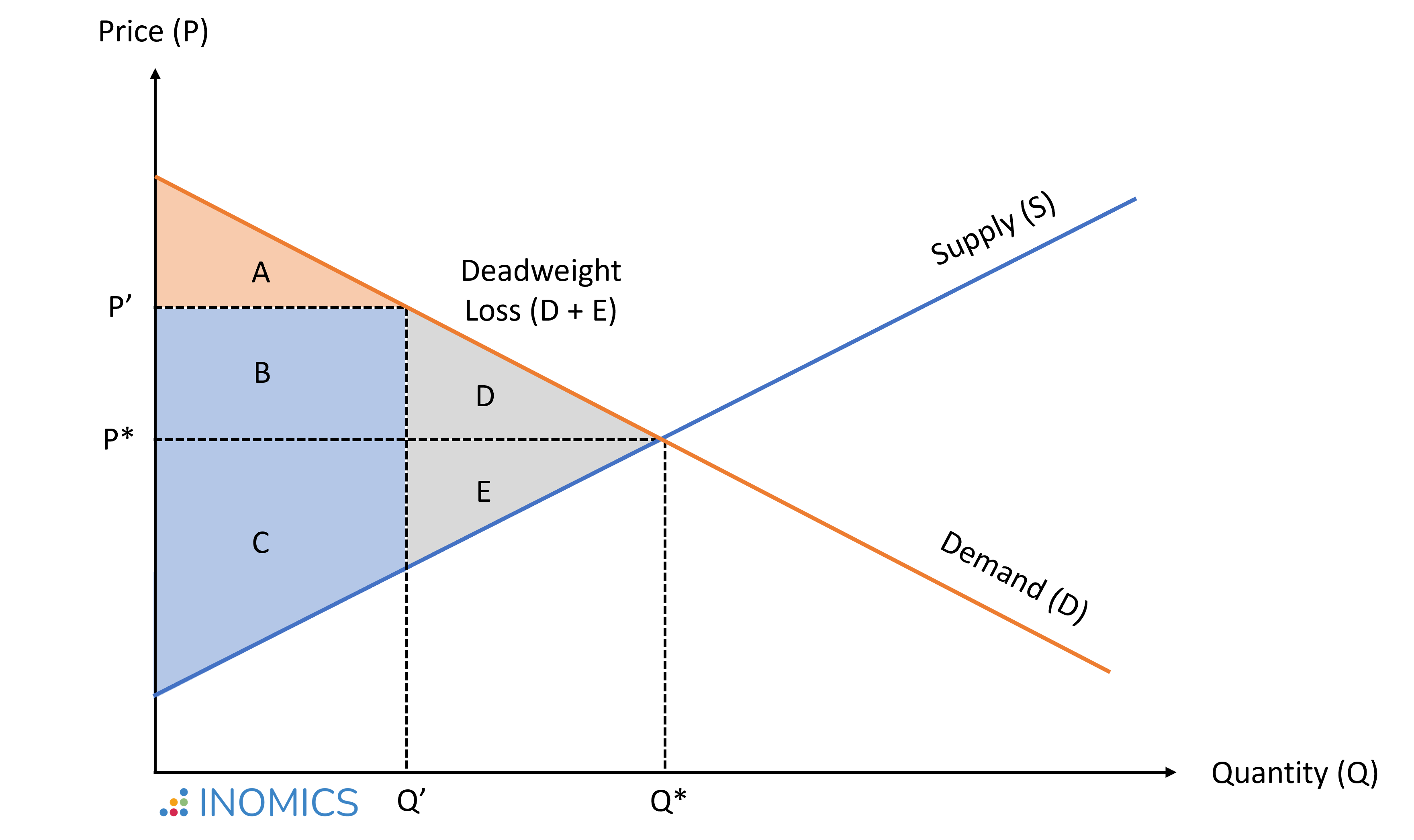
En caso de existir ineficiencias en el mercado, cuando la cantidad comerciada en el mercado difiere del resultado socialmente eficiente, el bienestar social permanece debajo del resultado óptimo. Por ejemplo, si el poder de mercado permite a los productores cobrar un precio P' > P*, la cantidad comerciada es reducida a Q' < Q*.

En esta situación, el excedente del consumidor (CS) es menor que en el equilibrio:

\begin{equation*}
             CS' = A < CS^* = A + B + D,
    \end{equation*}

mientras que el excedente del productor (PS) es mayor que en el equilibrio:

\begin{equation*}
             PS' = B + C > PS^* = C + E.
    \end{equation*}

Si bien el área B es transferida de consumidores a productores como consecuencia de un aumento en el precio, las áreas D + E reflejan la pérdida irrecuperable de eficiencia; es decir, el coste que la sociedad incurre y que se genera por la ineficiencia del mercado:

\begin{equation*}
            W^* - W' = (CS^* + PS^*)-(CS' + PS') = D + E. 
    \end{equation*}

En situaciones donde un fallo de mercado da lugar a una asignación de bienes y servicios ineficiente – al igual que la ilustrada anteriormente – es posible encontrar una asignación alternativa que mejore la situación de por lo menos una persona, sin tener que empeorar la situación de nadie más – mejorando así el bienestar social. En estas situaciones, la intervención del gobierno puede mejorar potencialmente el bienestar de todos. 

En el ejemplo anterior, si los precios y las cantidades se estableciesen en sus valores de equilibrio (P*, Q*), el gobierno podría establecer un impuesto de suma fija al consumidor con una importe igual a B. Por lo tanto, el gobierno podría proporcionar esta cantidad a los productores como un subsidio de suma fija, incrementando el excedente del consumidor al añadir el área D y el excedente del productor añadiendo el área E. Ésto eliminaría la pérdida irrecuperable de eficiencia; el excedente total sería el mismo que en el equilibrio competitivo. 

Asignaciones Pareto-Eficientes

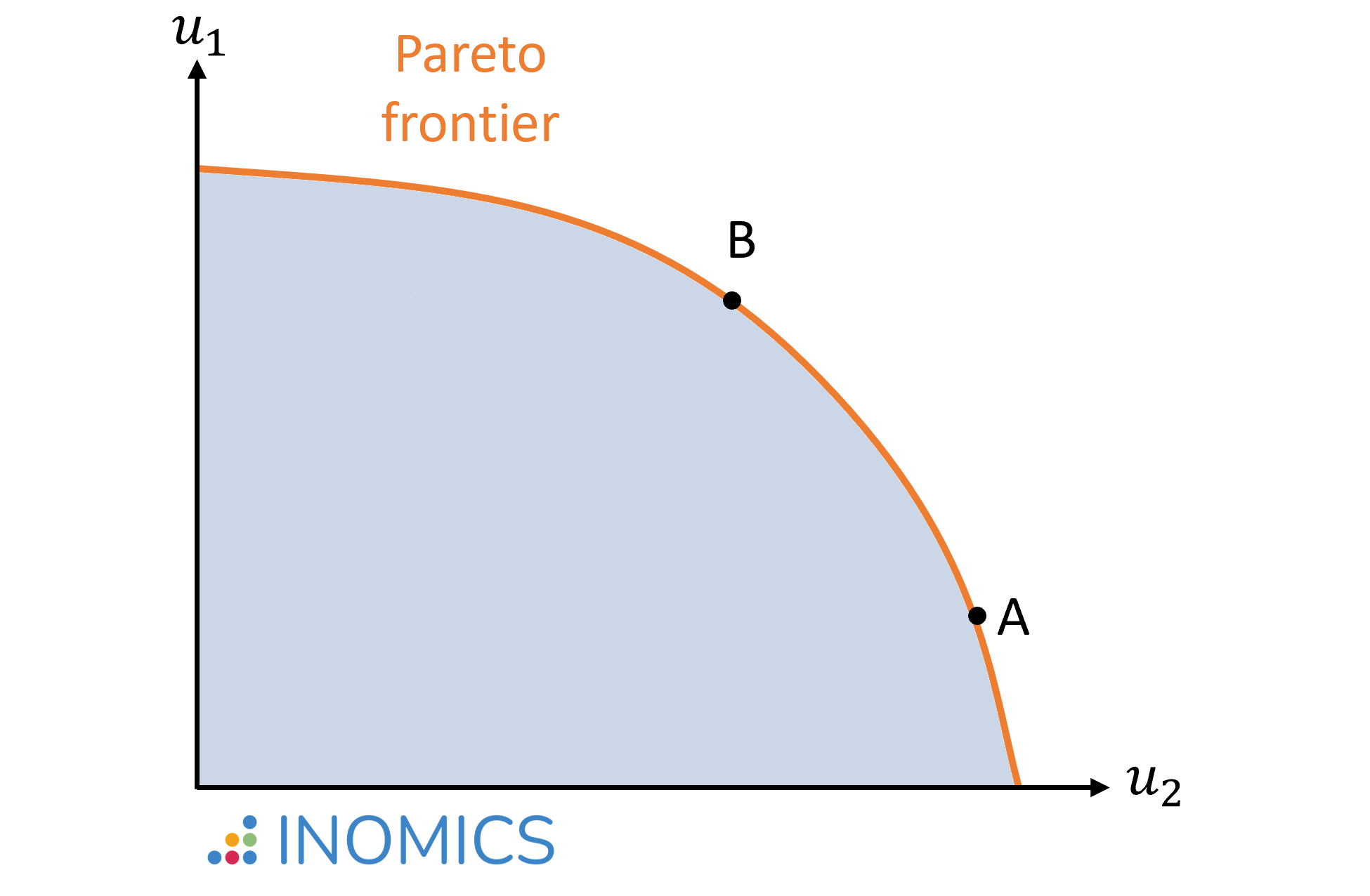
Se dice que una asignación es Pareto-eficiente (o Pareto-óptima) cuando no existe ningún otro intercambio viable que mejore por lo menos la situación de una persona sin tener que empeorar la de otra. 

El primer teorema de la economía del bienestar expone que cuando no existan (1) externalidades; y haya (2) competencia perfecta; (3) información perfecta (en lugar de información asimétrica); e (4) individuos completamente racionales, entonces todos los equilibrios competitivos son Pareto-eficientes. Estos equilibrios forman la frontera de Pareto (también llamada conjunto de Pareto). Ésta está ilustrada en el gráfico inferior en el caso de una economía con dos individuos (1 y 2). El área sombreada azul representa todas las combinaciones en la utilidad (u) que se podrían alcanzar factiblemente, sin embargo, éstas no son eficientes dado que hay recursos que no se utilizan. La curva naranja indica la frontera de Pareto, donde se utilizan todos los recursos y nadie puede mejorar su situación sin empeorar la de otro. 

Y, no menos importante, la Pareto-eficiencia define la optimalidad en un sentido limitado, y no da lugar a la "justicia" al clasificar distintas asignaciones Pareto-eficientes. Por ejemplo, no distingue entre los resultados A y B en el gráfico inferior, a pesar de que el resultado A genere una importante desigualdad en comparación con el resultado B.

​Función del Bienestar Social

Para clasificar distintas asignaciones de los recursos, de tal forma que sea conveniente para la sociedad, los economistas suelen emplear una función del bienestar social, W(u₁, u₂,...,u_H). La función del bienestar social no decrece en el bienestar individual, W'(u_H) > 0, y por lo tanto alcanza un máximo en cierta Pareto-optimalidad.

Para tener un ejemplo concreto, imagina la situación de una guardería, donde hay dos niños, Lisa (L) y Tom (T), y dos juguetes, un libro (B) y un puzle (P). El/la profesor/a está pensando en cómo distribuir los juguetes entre los niños. A ambos niños les gustan los juguetes, pero a Lisa le gustan más los puzles que los libros, mientras que a Tom le gustan los dos por igual. 

Supongamos que Lisa obtiene una utilidad u_L(P) = 5 al resolver el puzle, y una utilidad u_L(B) = 2 al leer el libro. Tom obtiene una utilidad u_T(P) = u_T(B) = 2 al realizar cualquiera de las dos actividades. Las siguientes asignaciones y las combinaciones de utilidad serían viables, asumiendo una utilidad agregada y una función del bienestar social. 

\begin{equation*}
     \text{Lisa: B,P; Tom:} \emptyset \quad \Rightarrow \quad 
     W = u_L(P,B) + u_T(\emptyset) = (5+2) + 0 = 7 \\
     \text{Lisa: B; Tom: P} \quad \Rightarrow \quad 
     W = u_L(B) + u_T(P) = 2 + 2 = 4 \\
     \text{Lisa: P; Tom: B} \quad \Rightarrow  \quad 
     W = u_L(P) + u_T(B) = 5 + 2 = 7 \\
     \text{Lisa: } \emptyset; \text{Tom: B,P} \quad \Rightarrow \quad 
     W = u_L(\emptyset) + u_T(P,B) = 0 + (2+2) = 4
    \end{equation*}

En este escenario, la segunda asignación no sería eficiente. Se puede alcanzar una mejora de Pareto intercambiando los juguetes: si Tom le da el puzle a Lisa y Lisa el libro a Tom, la utilidad de Lisa aumenta, mientras que la utilidad de Tom permanece igual. 

De forma similar, la cuarta asignación deja lugar a una mejora. Si Tom le diese el puzle a Lisa y se quedase solo con el libro, el bienestar agregado aumentaría. Sin embargo, la utilidad de Tom disminuiría a menos que se le compensase de alguna forma. Lisa podría compensarle por haberle regalado el puzle, ya que su mejora del bienestar derivada del intercambio es mayor que su pérdida de bienestar. 

Por ejemplo, Lisa podría ofrecerle a Tom leer el libro, si éste le diese el puzle. Si esta compensación C) trae consigo un coste de utilidad de u_L(C) < u_L(P) para Lisa y una mejora de la utilidad de u_T(C) ≥ u_T(P) para Tom, entonces se alcanzaría una mejora de Pareto mediante el `comercio' del puzle a cambio de la compensación. Si, digamos, que leerle el libro a Tom trae consigo un coste de utilidad de u_T(C) = 2 para Lisa y una mejora de la utilidad de u_T(C) = 2 para Tom, el bienestar agregado tras el intercambio sería W = u_L(P) - u_L(C) + u_T(B) + u_T(C) = (5-2) + (2+2) = 7. En un mercado con dinero, la solución más evidente sería tener a la Lisa adulta pagando al Tom adulto por el puzle por una cantidad u_T(P) ≤ x ≤ u_L(P).

Tanto la primera como la tercera asignación en el ejemplo descrito son Pareto-eficientes. No se puede mejorar la situación de ningún niño sin empeorar la del otro. Sin embargo, la clasificación de estas asignaciones depende de la forma funcional de la función del bienestar social. Hasta ahora, hemos asumido una estructura agregada: La utilidad de Lisa y la de Tom son sustitutos perfectos. 

Podríamos asumir también una estructura multiplicativa, en cuyo caso la utilidad de Lisa y la de Tom son complementos, y se penaliza la desigualdad. Ésto ocurre a menudo en la vida real, ya que el disfrute de prácticamente todo tiene rendimientos marginales decrecientes; una persona más pobre valora más un euro extra que una más rica. En este caso, la tercera asignación maximiza el bienestar social en la guardería. 

\begin{equation*}
     \text{Lisa: B,P; Tom:} \emptyset \quad \Rightarrow \quad 
     W = u_L(P,B) \times u_T(\emptyset) = (5+2) \times 0 = 0
    \end{equation*}

\begin{equation*}
     \text{Lisa: B; Tom: P} \quad \Rightarrow \quad 
     W = u_L(B) \times u_T(P) = 2 \times 2 = 4
    \end{equation*}

\begin{equation*}
     \text{Lisa: P; Tom: B} \quad \Rightarrow  \quad 
     W = u_L(P) \times u_T(B) = 5 \times 2 = 10
    \end{equation*}

\begin{equation*}
     \text{Lisa: } \emptyset; \text{Tom: B,P} \quad \Rightarrow \quad 
     W = u_L(\emptyset) \times u_T(P,B) = 0 \times (2+2) = 0
    \end{equation*}

De acuerdo con el segundo teorema del bienestar, cada Pareto-optimalidad se puede alcanzar mediante un equilibrio competitivo, si los impuestos de suma fija y las transferencias son instrumentos accesibles para cambiar las dotaciones individuales. Por ejemplo, si las dotaciones iniciales producen el punto A en el gráfico anterior y nuestra función del bienestar social prefiere el punto B, podemos imponer un impuesto de suma fija sobre el individuo 2 y dárselo al individuo 1 para provocar este cambio en el equilibrio resultante. 

En el ejemplo de la guardería, si Lisa decidiese coger el libro y el puzle (asignación 1), el/la profesor/a podría intervenir para quitarle el libro a Lisa y dárselo a Tom (asignación 2), cambiando de este modo entre dos asignaciones Pareto-eficientes para alcanzar la socialmente óptima. 

Desafortunadamente, en la práctica, la habilidad del gobierno de utilizar impuestos de suma fija para mejorar la distribución de recursos en una sociedad es limitada. Un impuesto de suma fija es una cantidad fija que los individuos pagan en función de sus características, independientemente de sus decisiones. Por ejemplo, imagina una economía con 10 personas, entre las cuales 5 tienen una riqueza inicial de 100€, mientras que las otras 5 tienen una riqueza inicial igual a 0€. Supongamos que el bienestar social se maximiza si aquellos con 100€ pagan con 50€ a quienes no tienen nada. 

Sin embargo, esta reasignación puede eliminar los incentivos de los individuos de generar riqueza en el futuro, si todos los beneficios se redistribuyen para compartirlos independientemente del esfuerzo de trabajo de cada individuo. Por otra parte, puede que el gobierno no observe directamente la información sobre la riqueza inicial. 

Conviene saber

En la práctica, las decisiones del gobierno rara vez se toman en situaciones donde las mejoras de Pareto son factibles. Más a menudo, el gobierno tendrá que abordar un compromiso entre los intereses y las necesidades de diferentes grupos, y las implicaciones de decisiones distintas sobre el bienestar agregado probablemente no se vean siempre con claridad. 

Por ejemplo, supongamos que el gobierno considera construir una nueva carretera. Aquellos que quieran utilizar la carretera para llegar más rápido al trabajo o para transportar los productos con más rapidez están dispuestos a pagar una tarifa de usuario, la cual cubre los costes de construcción y mantenimiento. A primera vista, la construcción de esta carretera puede parecer una mejora de Pareto: Claramente mejorará la situación de los individuos. 

Pero, es más probable que haya individuos que se vean adversamente afectados por la carretera. Las retenciones de tráfico y la congestión de vehículos pueden traer efectos secundarios negativos durante la construcción, y todos los vecindarios pueden acabar viéndose afectados negativamente por el ruido de la carretera. En este caso, aún seguiría siendo posible que el gobierno redujese los efectos positivos (construyendo un muro de protección acústica, por ejemplo) y/o compensase a aquellos que permaneciesen afectados negativamente. 

Equilibrar intereses en conflicto sería incluso más complejo en tiempos de crisis mayores, como la pandemia del COVID-19 ha destacado. Las estrategias en sí mismas empleadas para gestionar los riesgos de salud pública plantean riesgos. El sector de la atención sanitaria se enfrenta a riesgos en áreas no pandémicas debido al desvío de recursos para tratar y luchar contra el COVID-19. Mientras tanto, los negocios, las potenciales víctimas de violencia doméstica, y la educación de los niños son áreas donde los protocolos de respuesta a la pandemia pueden complicar una situación y empeorar la situación de determinados grupos en comparación a la media durante periodos de recuperación de la pandemia. 

La información de los expertos puede ayudar a clarificar algunos de estos compromisos, aunque comparando los beneficios y las pérdidas individuales derivados de cada política, y encontrar la solución socialmente óptima, será menos sencillo que lo que sugieren los simples ejemplos presentados anteriormente.