L'économie du bien-être est l'étude de la manière dont une allocation donnée des biens et des ressources dans une société affecte le bien-être économique. Elle cherche à orienter les politiques publiques vers une répartition qui profite à l'ensemble de la société. À ce titre, elle fournit les outils permettant de comparer différentes allocations de ressources et de les évaluer du point de vue du bien-être social - ou, en termes simples, de juger du caractère "équitable" de ces allocations. Trois concepts fondamentaux sont utilisés dans l'analyse du bien-être : le surplus total, l'efficacité de la répartition et la fonction de bien-être social.

​Excédent total

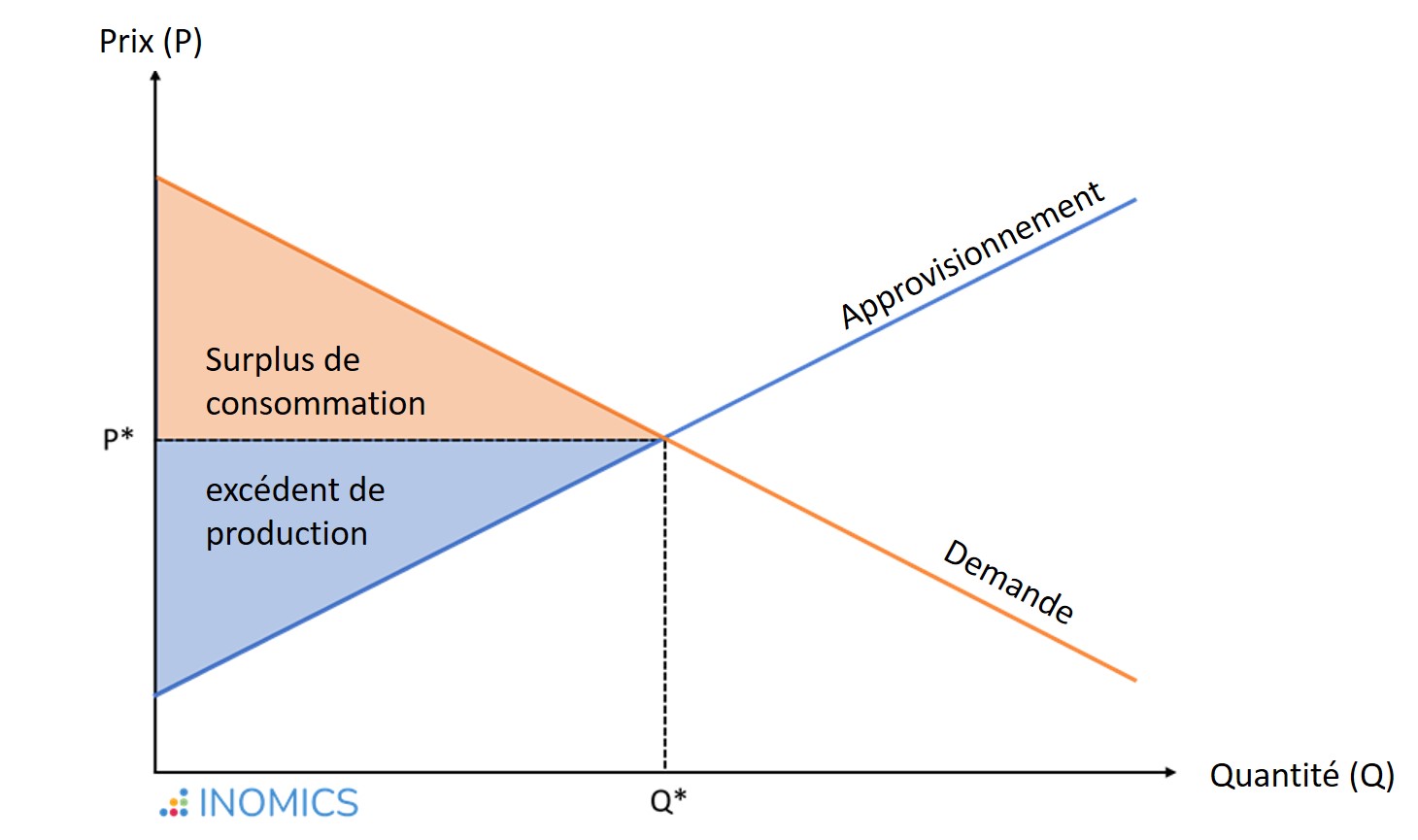
Dans un modèle stylisé, le surplus total du marché représente le bien-être total de tous les participants à un marché. Il s'agit de la somme du surplus du consommateur et du surplus du producteur, qui peut être considéré comme le gain net pour la société de tous les échanges (ou transactions) effectués sur ce marché.

• Le surplus du consommateur d'un individu est la différence entre le prix le plus élevé qu'il est prêt à payer pour un produit et le prix qu'il paie effectivement. La zone située sous la courbe de demande et au-dessus du prix du marché est le surplus du consommateur total additionné pour tous les consommateurs du marché.
• Le surplus d'un producteur est la différence entre le prix le plus bas qu'il serait prêt à accepter, compte tenu des coûts de production, et le prix auquel le produit est effectivement vendu. La zone située au-dessus de la courbe d'offre du marché et au-dessous du prix du marché est le surplus total du producteur additionné pour tous les producteurs du marché.

Dans l'équilibre du marché où l'offre est égale à la demande (noté P* et Q* dans la figure ci-dessous), la somme des surplus du consommateur et du producteur - et donc le bien-être total - est maximisée.

​En cas d'inefficacité du marché, lorsque la quantité négociée sur le marché s'écarte du résultat socialement efficace, le bien-être social reste inférieur au résultat optimal. Par exemple, si le pouvoir de marché permet aux producteurs de pratiquer un prix P' > P*, la quantité échangée est réduite à Q' < Q*.

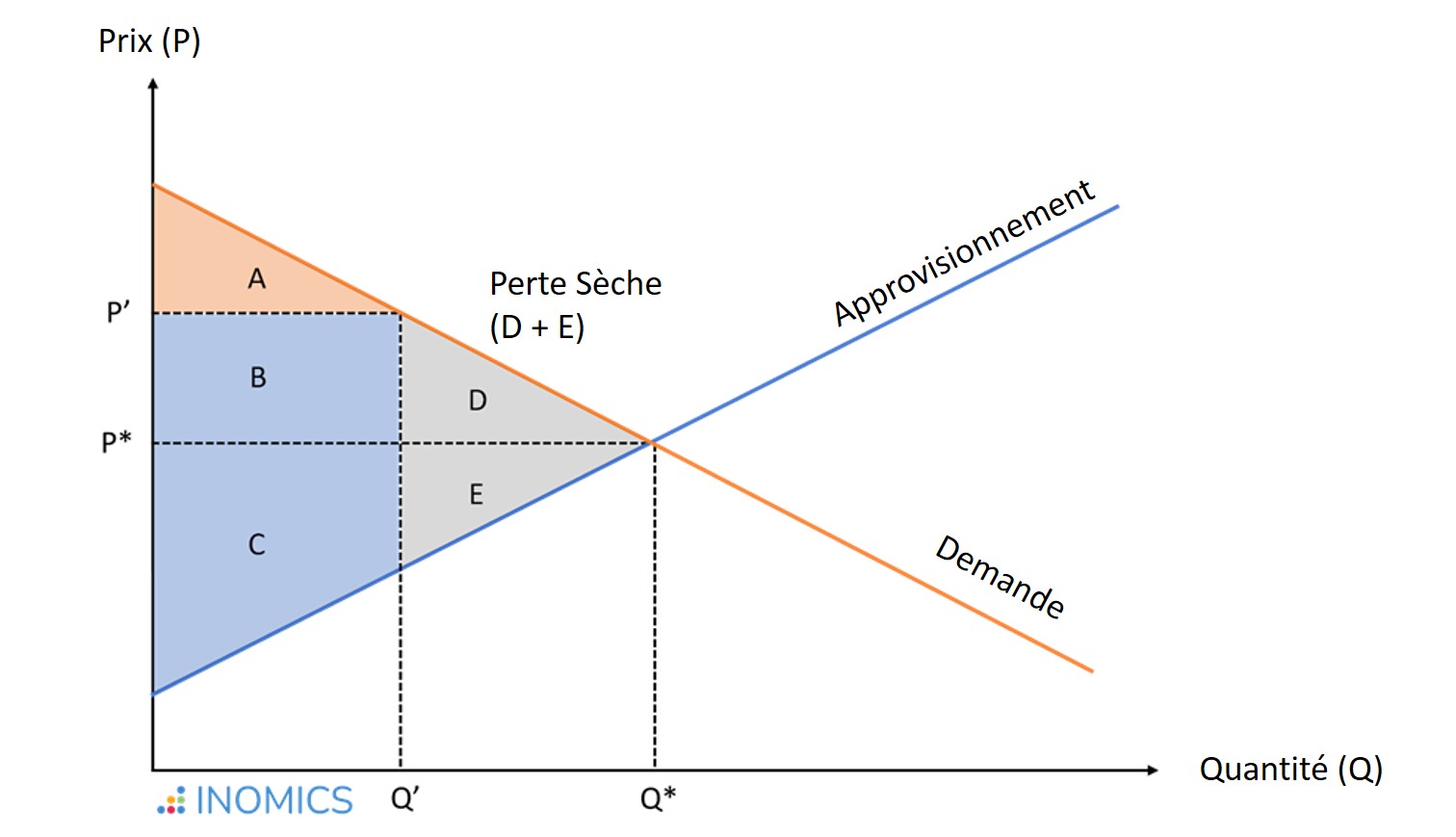
Dans cette situation, le surplus du consommateur (CS) est plus faible qu'à l'équilibre :

\begin{equation*}
             CS' = A < CS^* = A + B + D,
    \end{equation*}

while the producer surplus (PS) is higher than in equilibrium:

\begin{equation*}
             PS' = B + C > PS^* = C + E.
    \end{equation*}

Alors que la zone B est transférée des consommateurs aux producteurs à la suite d'une augmentation des prix, les zones D et E reflètent la perte de bien-être due à l'effet d'aubaine, c'est-à-dire le coût pour la société engendré par l'inefficacité du marché :

\begin{equation*}
            W^* - W' = (CS^* + PS^*)-(CS' + PS') = D + E. 
    \end{equation*}

Dans les situations où la défaillance du marché entraîne une distribution inefficace des biens et des services - comme celle illustrée ci-dessus - il est possible de trouver une répartition alternative qui améliore la situation d'au moins une personne, sans détériorer celle des autres - améliorant ainsi le bien-être social. Dans ces situations, l'intervention des pouvoirs publics peut potentiellement améliorer le bien-être de tous.

Dans l'exemple ci-dessus, si les prix et les quantités étaient fixés aux valeurs d'équilibre (P*, Q*), le gouvernement pourrait prélever une taxe forfaitaire à la consommation de la taille de la zone B. Ensuite, il pourrait fournir ce montant sous forme de subvention forfaitaire aux producteurs, augmentant le surplus du consommateur de la zone D et le surplus du producteur de la zone E. Cela éliminerait la perte sèche. Il pourrait ensuite verser ce montant sous la forme d'une subvention forfaitaire aux producteurs, ce qui augmenterait le surplus du consommateur de la zone D et le surplus du producteur de la zone E. Cela éliminerait la perte sèche ; le surplus total serait le même que dans l'équilibre concurrentiel.

Allocations efficaces au sens de Pareto

Il est répondu qu'une allocation est efficace (ou optimale) au sens de Pareto lorsqu'aucun autre échange n'est possible qui améliorerait la situation d'au moins une personne sans aggraver celle d'une autre.

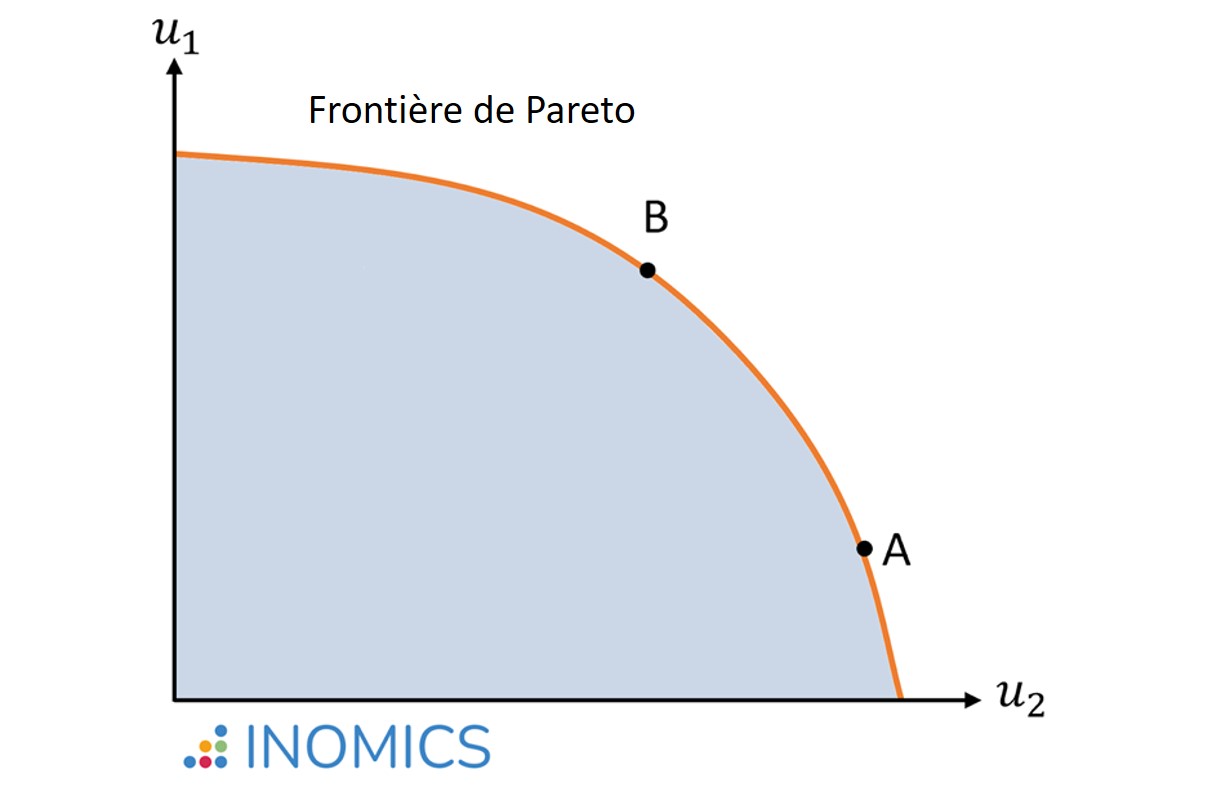
Le premier théorème de l'économie du bien-être stipule que lorsqu'il existe (1) aucune externalité, (2) une concurrence parfaite, (3) une information parfaite (au lieu d'une information asymétrique) et (4) des agents pleinement rationnels, tous les équilibres concurrentiels sont efficaces au sens de Pareto. Ces équilibres forment la frontière de Pareto (également appelée ensemble de Pareto). Ceci est illustré dans la figure ci-dessous pour une économie à deux agents (1 et 2). La zone ombrée en bleu représente toutes les combinaisons d'utilité (u) qu'il serait possible d'atteindre, mais qui ne sont pas efficientes puisque des ressources restent inutilisées. La ligne orange indique la frontière de Pareto, où toutes les ressources sont utilisées et où personne ne peut voir sa situation s'améliorer sans que celle d'un autre ne s'aggrave.

Il est important de noter que l'efficacité de Pareto ne définit l'optimalité que dans un sens limité, car elle ne permet pas d'établir un classement "équitable" entre les différentes allocations efficaces de Pareto. Par exemple, elle ne fait pas de distinction entre les résultats A et B dans la figure ci-dessous, même si le résultat A génère une inégalité substantielle par rapport au résultat B.

Fonction sociale

Pour classer les différentes allocations de ressources en fonction de leur désirabilité sociale, les économistes utilisent généralement une fonction de bien-être social, W(u₁ , u₂ ,...,u_H ). La fonction de bien-être social est non décroissante dans le bien-être individuel, W'(u_H ) > 0, et atteint donc un maximum à un certain optimum de Pareto.

Pour donner un exemple plus concret, imaginons une situation dans une garderie. Il y a deux enfants, Lisa (L) et Tom (T), et deux jouets, un livre (B) et un puzzle (P). L'enseignant réfléchit à la manière de répartir les jouets entre les enfants. Les deux enfants aiment les deux jouets, mais Lisa préfère les puzzles aux livres, tandis que Tom aime les deux à égalité.

Supposons que Lisa tire une utilité u_L (P) = 5 de la résolution de l'énigme et une utilité u_L (B) = 2 de la lecture du livre. Tom tire une utilité u_T (P) = u_T (B) = 2 de l'une ou l'autre activité. Les allocations et combinaisons d'utilité suivantes seraient réalisables, en supposant une fonction d'utilité et de bien-être social additive :

\begin{equation*}
     \text{Lisa: B,P; Tom:} \emptyset \quad \Rightarrow \quad 
     W = u_L(P,B) + u_T(\emptyset) = (5+2) + 0 = 7 \\
     \text{Lisa: B; Tom: P} \quad \Rightarrow \quad 
     W = u_L(B) + u_T(P) = 2 + 2 = 4 \\
     \text{Lisa: P; Tom: B} \quad \Rightarrow  \quad 
     W = u_L(P) + u_T(B) = 5 + 2 = 7 \\
     \text{Lisa: } \emptyset; \text{Tom: B,P} \quad \Rightarrow \quad 
     W = u_L(\emptyset) + u_T(P,B) = 0 + (2+2) = 4
    \end{equation*}

Dans ce contexte, la deuxième allocation ne serait pas efficace. En échangeant les jouets, une amélioration de Pareto peut être obtenue : Si Tom donne le puzzle à Lisa et que Lisa donne le livre à Tom, l'utilité de Lisa augmente, tandis que celle de Tom reste inchangée.

De la même manière, la quatrième allocation peut être améliorée. Si Tom donnait le puzzle à Lisa et ne gardait que le livre, le bien-être global augmenterait. Cependant, l'utilité de Tom diminuerait à moins qu'il ne soit compensé d'une manière ou d'une autre. Lisa pourrait dédommager Tom pour avoir donné le puzzle, car son gain de bien-être résultant de l'échange est plus important que sa perte de bien-être.

Par exemple, Lisa pourrait proposer de lire le livre à Tom s'il lui donne le puzzle. Si cette compensation (C) entraîne un coût d'utilité de u_L (C) < u_L (P) pour Lisa et un gain d'utilité de u_T (C) ≥ u_T (P) pour Tom, alors une amélioration de Pareto est atteinte en "échangeant" le puzzle contre une compensation. Si, par exemple, la lecture du livre à Tom entraîne un coût d'utilité de u_T (C) = 2 pour Lisa et un gain d'utilité de u_T (C) = 2 pour Tom, le bien-être global après l'échange serait W = u_L (P) - u_L (C) + u_T (B) + u_T (C) = (5-2) + (2+2) = 7. Dans un marché avec monnaie, la solution évidente est que Lisa adulte paie Tom adulte pour le puzzle pour un montant u_T (P) ≤ x ≤ u_L (P).

La première et la troisième allocation de la liste d'exemples ci-dessus sont toutes deux efficaces au sens de Pareto. Aucun enfant ne peut être mieux loti sans que l'autre ne le soit moins. Cependant, le classement de ces allocations dépend de la forme fonctionnelle de la fonction de bien-être social. Jusqu'à présent, nous avons supposé une structure additive : Les utilités de Lisa et de Tom sont des substituts parfaits.

Nous pourrions également supposer une structure multiplicative, auquel cas l'utilité de Lisa et de Tom sont des suppléments, et l'inégalité est pénalisée. C'est typiquement le cas dans la vie réelle, puisqu'il existe des rendements marginaux décroissants pour la jouissance de presque tout ; une personne plus pauvre accorde plus de valeur à un euro supplémentaire qu'une personne riche. Dans ce cas, la troisième allocation maximise le bien-être social à la garderie :

\begin{equation*}
     \text{Lisa: B,P; Tom:} \emptyset \quad \Rightarrow \quad 
     W = u_L(P,B) \times u_T(\emptyset) = (5+2) \times 0 = 0
    \end{equation*}

\begin{equation*}
     \text{Lisa: B; Tom: P} \quad \Rightarrow \quad 
     W = u_L(B) \times u_T(P) = 2 \times 2 = 4
    \end{equation*}

\begin{equation*}
     \text{Lisa: P; Tom: B} \quad \Rightarrow  \quad 
     W = u_L(P) \times u_T(B) = 5 \times 2 = 10
    \end{equation*}

\begin{equation*}
     \text{Lisa: } \emptyset; \text{Tom: B,P} \quad \Rightarrow \quad 
     W = u_L(\emptyset) \times u_T(P,B) = 0 \times (2+2) = 0
    \end{equation*}

Selon le deuxième théorème du bien-être, chaque optimum de Pareto peut être atteint par le biais d'un équilibre concurrentiel, si des taxes et des transferts forfaitaires sont disponibles pour modifier les dotations individuelles. Par exemple, si les dotations initiales donnent le point A dans la figure ci-dessus et que notre fonction de bien-être social préfère le point B, nous pouvons imposer un impôt forfaitaire à l'individu 2 et le donner à l'individu 1 pour induire ce changement dans l'équilibre résultant.

Dans l'exemple de la garderie, si Lisa décide de prendre le livre et le puzzle (allocation 1), l'enseignant pourrait intervenir et retirer le livre à Lisa pour le donner à Tom (allocation 2), passant ainsi d'une allocation efficace au sens de Pareto à une allocation socialement optimale.

 Malheureusement, dans la pratique, la capacité du gouvernement à utiliser des impôts forfaitaires pour améliorer la distribution des ressources dans une société est limitée. Un impôt forfaitaire est un montant fixe que les individus paient en fonction de leurs caractéristiques, indépendamment de leurs choix. Par exemple, imaginons une économie de 10 personnes, dont 5 ont une richesse initiale de 100 €, tandis que les 5 autres ont une richesse initiale de 0 €. Supposons que le bien-être social soit maximisé si ceux qui ont 100 € versent 50 € à ceux qui n'ont rien.

Toutefois, cette réaffectation peut éliminer les incitations des individus à générer des richesses futures, si tous les gains sont redistribués pour être partagés de manière égale, indépendamment de l'effort de travail de chaque individu. De plus, l'information sur la richesse initiale peut ne pas être directement observable par le gouvernement.

Bon à savoir

Dans la pratique, les décisions des pouvoirs publics sont rarement prises dans des situations où des améliorations de Pareto sont possibles. Le plus souvent, le gouvernement est confronté à un trading entre les besoins et les intérêts de différents groupes, et les implications de différentes décisions sur le bien-être global ne sont pas toujours claires.

Supposons par exemple que le gouvernement envisage de construire une nouvelle autoroute. Ceux qui souhaitent l'emprunter pour arriver plus vite au travail ou transporter leurs produits plus rapidement sont prêts à payer un droit d'usage qui couvrirait les coûts de construction et d'entretien. À première vue, la construction de cette autoroute peut sembler être une amélioration de Pareto : Il est clair qu'elle améliorera la situation de certains individus.

Mais il y aura très probablement aussi des personnes qui subiront les effets négatifs de l'autoroute. Les retards de circulation et les embouteillages peuvent avoir des effets secondaires négatifs pendant la construction, et des quartiers entiers peuvent rester affectés par le bruit de l'autoroute. Dans ce cas, il est encore possible pour le gouvernement de réduire les effets négatifs (par exemple, en construisant un mur de protection contre le bruit) et/ou d'indemniser les personnes qui restent affectées.

L'équilibre entre des intérêts contradictoires sera encore plus difficile à trouver en période de crise majeure, comme l'a montré la pandémie de COVID-19. Les stratégies utilisées pour gérer les risques de santé publique présentent elles-mêmes des risques. Le secteur des soins de santé est confronté à des risques dans les zones non pandémiques en raison du détournement des ressources pour traiter et combattre le COVID-19. Par ailleurs, les entreprises, les victimes potentielles de violences domestiques et l'éducation des enfants sont autant de domaines dans lesquels les protocoles de réponse à la pandémie peuvent compliquer la situation et rendre certains groupes relativement moins bien lotis que la moyenne pendant les périodes de reprise de la pandémie.

L'avis d'un expert peut aider à clarifier certains de ces compromis, mais la comparaison des gains et des pertes individuels découlant de chaque option politique et la recherche de la solution socialement optimale seront moins simples que ne le suggèrent les exemples simples présentés ci-dessus.