L'élasticité de substitution mesure la facilité avec laquelle on peut passer d'un facteur de production à un autre. Le concept a un large éventail d'applications, allant de la comparaison du travail et du capital dans les entreprises, des travailleurs immigrés par rapport aux travailleurs autochtones sur le marché du travail, jusqu’à l'évaluation des méthodes de production "propres" par rapport aux méthodes "sales" pour l'économie de l'environnement.

Afin de calculer une élasticité de substitution, il est d'abord nécessaire de déterminer un isoquant et de calculer les ratios d’inputs et les taux marginaux de substitution technique le long de l'isoquant. Un isoquant représente les combinaisons d’inputs \(x_{1}\) et \(x_{2}\) nécessaires pour produire un niveau d’output donné \(\overline{Y}\), comme les combinaisons le long de l'isoquant bleu \(f\left(x_{1},x_{2}\right)=\overline{Y}\) dans le graphique ci-dessous. Pour tout point donné \(\left(x_{1},x_{2}\right)\) de l'isoquant \(f\left(x_{1},x_{2}\right)=\overline{Y}\), il est possible de calculer le ratio d’input, qui est simplement la quantité d'un input divisée par un autre \(\frac{x_{2}}{x_{1}}\), comme le montrent les gradients des lignes roses et grises du graphique. Toute technique de production qui utilise les inputs \(x_{1}\) et \(x_{2}\) pour obtenir l’output \(\overline{Y}\) aura un ratio d’input spécifique à cette technique particulière. Pour tout point donné \(\left(x_{1},x_{2}\right)\) sur l'isoquant \(f\left(x_{1},x_{2}\right)=\overline{Y}\) on peut également calculer le taux marginal de substitution technique \(\frac{-dx_{2}}{dx_{1}}\), qui est le taux auquel l’input \(x_{1}\) peut être échangée contre l’input \(x_{2}\) tout en maintenant le niveau de l’output à \(\overline{Y}\).

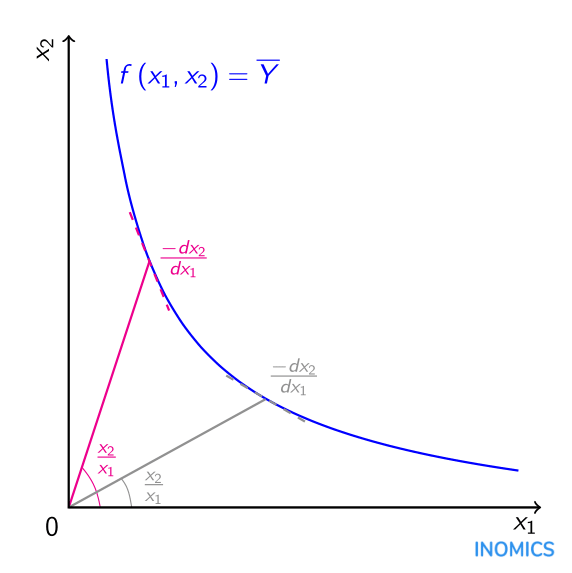
En substance, l'élasticité de substitution \(\sigma\) mesure la facilité avec laquelle on peut se déplacer entre les points le long d'un isoquant. Lorsque l'on se déplace entre ces points, il y a des changements à la fois dans le ratio d’input et le taux marginal de substitution technique. L'élasticité de substitution établit des changements proportionnels dans le ratio d’input par rapport aux changements proportionnels dans le taux marginal de substitution technique de telle sorte que : \[\sigma=\frac{\frac{\Delta\left(x_{2}/x_{1}\right)}{x_{2}/x_{1}}}{\frac{\Delta\left(-dx_{2}/dx_{1}\right)}{-dx_{2}/dx_{1}}}.\] 

Une valeur positive de indique un certain degré de substituabilité entre les inputs de production. Dans le cas extrême des substituts parfaits, l'élasticité de substitution approche l'infini. L'électricité provenant de deux fournisseurs différents pourrait être considérée comme un exemple de substitut parfait : l'électricité fait le même travail d'alimentation de la production, quel que soit le fournisseur. En revanche, une valeur de \(\sigma=0\) indique exactement le contraire : les inputs ne peuvent se substituer l'un à l'autre, ils sont même parfaitement complémentaires ; l'un ne peut être employé sans employer également l'autre. Par exemple, dans la production automobile, les roues nécessitent des pneus ; aucun des deux ne suffit à lui seul. Ainsi, les roues et les pneus sont des compléments parfaits.

En général, l'élasticité de substitution change à différents points le long d'un isoquant. Par exemple, il peut être plus difficile d'échanger des machines contre des personnes (low \(\sigma\)) lorsque seules quelques personnes sont impliquées dans la production, alors qu'il est plus facile d'introduire des machines (high \(\sigma\)) lorsqu'il y a encore suffisamment de personnes pour faire fonctionner les machines. Cependant, il existe un cas particulier où l'élasticité de substitution est à un niveau constant pour toute combinaison d'inputs de production. C'est-à-dire que \(\sigma\) a la même valeur à n'importe quel point le long des isoquants qui représentent la fonction de production. Dans la pratique, cela est quelque peu irréaliste mais simplifie considérablement les mathématiques, en particulier pour la modélisation empirique, et c'est pourquoi l'hypothèse d'une elasticité de substitution constante (ou CES, de l’anglais “Constant Elasticity of Substitution”) est populaire parmi les économistes qui étudient la production. L'exemple le plus connu d'une fonction de production CES est la fonction de production de Cobb-Douglas.

La décision sur la manière d'organiser la production dépend à la fois de la substituabilité des facteurs de production (valeur de \(\sigma\), forme des isoquants) et du coût relatif des inputs les uns par rapport aux autres, qui peut être représenté au moyen de lignes d'isocoûts. Par exemple, si une entreprise énergétique produit de l'électricité à la fois à partir d'une source écologique (le vent par exemple) et en brûlant un combustible carboné, la part de chaque input (vent ou combustible carboné) que l'entreprise alloue à la production d'électricité sera ramenée à son coût relatif. Bien entendu, si l'entreprise a la mauvaise réputation de nuire à l'environnement, le coût lié à sa réputation pourrait également être intégré dans le coût de production, ce qui augmenterait la probabilité que l'entreprise choisisse ou augmente son utilisation de la source verte. Le gouvernement pourrait également chercher à réguler le marché de l'électricité. (Nous vous conseillons de consulter les articles sur les défaillances du marché et les externalités positives et négatives)

En savoir plus

Pour une application de l'élasticité de substitution à la théorie de l'économie de l'environnement, consultez le document des économistes Daron Acemoglu, Philippe Aghion, Leonardo Bursztyn et David Hemous, "The environment and directed technical change" (American Economic Review, 2012). Les auteurs comparent les technologies "propres" et "sales" dans le cadre d'un modèle de croissance durable, en proposant des recommandations pour différents types d'intervention publique qui dépendent de la substituabilité des inputs.

Bon à savoir

Le concept d'élasticité de substitution est également applicable à la théorie de la demande, pour l'analyse des courbes d'indifférence et de la substituabilité des biens et services dans la consommation. Le concept remonte au début des années 1930, lorsqu'il a été initialement développé simultanément et indépendamment par les économistes John Hicks et Joan Robinson. Ironiquement, on pourrait dire que Hicks et Robinson étaient de bons substituts l'un de l'autre dans la production de connaissances économiques, avec une valeur mutuellement élevée de \(\sigma\) ! Néanmoins, du point de vue de l'étudiant, une bonne compréhension de ce concept nécessite un certain effort. Comme Thomas Edison l'a dit un jour, “there is no substitute for hard work” (rien ne remplace le travail acharné).