Die Substitutionselastizität ist ein Maß dafür, wie leicht zwischen Produktionsfaktoren gewechselt werden kann. Das Konzept wird vielfältig angewendet, etwa um zu messen, wie Arbeit und Kapital im Unternehmen ausgetauscht werden können, wie einheimische Arbeitskräfte durch eingewanderte Arbeitskräfte auf dem Arbeitsmarkt ersetzt werden können oder wie im Bereich der Umweltökonomie "schmutzige" Produktionsmethoden durch "saubere"  abgelöst werden können.

Um die Substitutionselastizität zu berechnen, ist es notwendig, zuerst eine Isoquante zu bestimmen und die Input-Verhältnisse wie auch die Grenzraten der technischen Substitution entlang der Isoquante zu berechnen. Eine Isoquante stellt die Kombinationen der Inputs \(x_{1}\) und \(x_{2}\) dar, die erforderlich sind, um ein bestimmtes Produktionsniveau \(\overline{Y}\) zu produzieren, wie zum Beispiel die Kombinationen entlang der blauen Isoquante \(f\left(x_{1},x_{2}\right)=\overline{Y}\) in der Grafik unten. Für jeden beliebigen Punkt \(\left(x_{1},x_{2}\right)\) auf der Isoquante \(f\left(x_{1},x_{2}\right)=\overline{Y}\) kann das jeweilige Inputverhältnis berechnet werden, indem die Menge des einen Inputs durch die Menge des anderen Inputs geteilt wird \(\frac{x_{2}}{x_{1}}\), so wie es in der Grafik durch die Steigung der pinken und der grauen Linie dargestellt wird. Jede Produktionstechnik, die die Inputs \(x_{1}\) und \(x_{2}\) verwendet, um den Output \(\overline{Y}\) zu erzielen, wird ein für genau diese Technik spezifisches Inputverhältnis verwenden. Für jeden gegebenen Punkt \(\left(x_{1},x_{2}\right)\) auf der Isoquante \(f\left(x_{1},x_{2}\right)=\overline{Y}\) kann auch die Grenzrate der technischen Substitution \(\frac{-dx_{2}}{dx_{1}}\) berechnet werden. Die GRTS sagt aus, in welchem Verhältnis Input \(x_{1}\) gegen Input \(x_{2}\) ausgetauscht werden kann, während das Niveau des Outputs bei \(\overline{Y}\) bleibt.

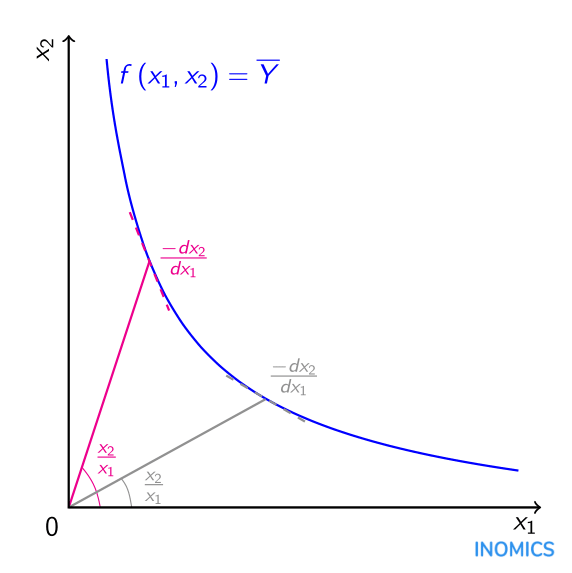
Im Wesentlichen misst die Substitutionselastizität \(\sigma\) wie leicht es ist, sich zwischen verschiedenen Punkten entlang einer Isoquante zu bewegen. Wenn man sich entlang der Isoquante bewegt, ändert sich sowohl das Inputverhältnis, als auch die Grenzrate der technischen Substitution. Die Substitutionselastizität setzt anteilige Änderungen im Inputverhältnis in Beziehung zu anteiligen Änderungen in der Grenzrate der technischen Substitution, sodass 

\[\sigma=\frac{\frac{\Delta\left(x_{2}/x_{1}\right)}{x_{2}/x_{1}}}{\frac{\Delta\left(-dx_{2}/dx_{1}\right)}{-dx_{2}/dx_{1}}}.\]

Ein positiver Wert von \(\sigma\) zeigt einen bestimmten Grad der Substituierbarkeit zwischen den Produktionsinputs an. Im Extremfall perfekter Substitute geht die Substitutionselastizität gegen unendlich \(\sigma\rightarrow\infty\). Ein Beispiel für ein perfektes Substitut ist etwa Strom von zwei verschiedenen Anbietern: Der Strom treibt gleichermaßen die Produktion eines Guts an, unabhängig vom Anbieter. Ein Wert von \(\sigma=0\) impliziert genau das Gegenteil: Die Inputs können einander nicht substituieren, sie sind vielmehr perfekte Komplemente; ein Inputfaktor kann nicht eingesetzt werden, ohne dass nicht auch der andere Inputfaktor eingesetzt wird. Bei der Autoproduktion beispielsweise benötigen Räder auch Reifen; keines der beiden Inputs ist für sich allein ausreichend. Somit sind Räder und Reifen perfekte Komplemente.

Im Allgemeinen ändert sich die Substitutionselastizität an den verschiedenen Punkten entlang einer Isoquante. Zum Beispiel ist es möglicherweise schwieriger, Maschinen gegen Menschen auszutauschen (low \(\sigma\)), wenn in der Ausgangssituation nur wenige Menschen an der Produktion beteiligt sind. Während es dann einfacher ist mehr Maschinen einzusetzen (high \(\sigma\)), solange es in der Ausgangssituation noch viele Menschen gibt, die die Maschinen bedienen können. Falls die Substitutionselastizität für jede Kombination der Produktionsinputs auf einem konstanten Niveau liegt, haben wir einen Sonderfall. Dann hat \(\sigma\) an jedem Punkt entlang der Isoquante, die die Produktionsfunktion abbildet, den gleichen Wert. In der Praxis ist das zwar etwas unrealistisch, für die empirische Modellierung vereinfacht es jedoch die Mathematik erheblich. Daher ist die Annahme einer konstanten Substitutionselastizität (Englisch: Constant Elasticity of Substitution, CES) unter Ökonomen zur Untersuchung der Produktion sehr beliebt. Das bekannteste Beispiel für eine CES-Produktionsfunktion ist die Cobb-Douglas Produktionsfunktion.

Die Entscheidung über die Organisation der Produktion hängt sowohl von der Substituierbarkeit der Produktionsinputs (Wert von \(\sigma\), Form der Isoquanten) als auch von den relativen Kosten der Inputs zueinander ab, die durch Isokostengeraden dargestellt werden können. Nehmen wir als Beispiel ein Energieunternehmen, das Strom sowohl durch eine umweltfreundliche Quelle (z. B. Wind), als auch durch die Verbrennung von Kohle produziert. Dann hängt die Entscheidung, wie viel von jedem Input (Wind oder Kohle) das Unternehmen zur Stromproduktion einsetzt, von den relativen Kosten der Inputs ab. Wenn das Unternehmen aufgrund seiner Energieproduktion mittels Kohleverbrennung einen schlechten Ruf hat, weil es die Umwelt schädigt, könnten die Reputationskosten auch zu den Produktionskosten gezählt werden. Das würde die Wahrscheinlichkeit erhöhen, dass das Unternehmen sich für die umweltfreundliche Variante entscheidet oder zumindest den Anteil der Produktion an der umweltfreundlichen Variante erhöht. Alternativ könnte die Regierung auch versuchen, den Strommarkt zu regulieren.

Zum Weiterlesen

Im Paper "The environment and directed technical change" (American Economic Review, 2012) der Ökonomen Daron Acemoglu, Philippe Aghion, Leonardo Bursztyn und David Hemous wird das Konzept der Substitutionselastizität auf die Umweltökonomie angewendet. Die Autoren vergleichen "saubere" und "schmutzige" Technologien im Rahmen eines Modells des nachhaltigen Wachstums und geben verschiedene Empfehlungen für Arten von staatlichen Eingriffen, je nach Substituierbarkeit der Inputs.

Gut zu Wissen

Das Konzept der Substitutionselastizität kann auch in der Nachfragetheorie angewendet werden, dort wird es für die Analyse von Indifferenzkurven und für die Substituierbarkeit von Gütern und Dienstleistungen im Konsum verwendet. Das Konzept stammt aus den frühen 1930er Jahren, zu der Zeit wurde es von zwei Ökonomen gleichzeitig und unabhängig voneinander entwickelt, nämlich von John Hicks und Joan Robinson. Ironischerweise könnte man sagen, dass Hicks und Robinson in der Produktion von ökonomischem Wissen in diesem Fall Substitute zueinander waren, mit einem hohen Wert von \(\sigma\)! Ein umfangreiches Verständnis dieses Konzepts erfordert nichtsdestotrotz einige Anstrengungen von Seiten des Lernenden. Thomas Edison sagte einmal, es gibt kein Substitut zu harter Arbeit.