La elasticidad de sustitución mide la facilidad con la cual uno puede cambiar entre factores de producción. El concepto abarca una amplia serie de aplicaciones, desde comparaciones entre el trabajo y el capital en las empresas, inmigrantes frente a trabajadores nativos en el mercado de trabajo, hasta valorar métodos de producción ‘limpios’ frente a ‘sucios’ en la economía medioambiental.

Para calcular una elasticidad de sustitución, primero es necesario determinar una isocuanta y calcular relaciones de insumos y relaciones marginales de sustitución técnica a lo largo de la isocuanta. Una isocuanta representa combinaciones de insumos \(x_{1}\) y \(x_{2}\) requeridos para producir un nivel de producción dado \(\overline{Y}\), tal y como las combinaciones a lo largo de la isocuanta azul \(f\left(x_{1},x_{2}\right)=\overline{Y}\) en el gráfico de más abajo. Para cualquier punto dado \(\left(x_{1},x_{2}\right)\) en la isocuanta \(f\left(x_{1},x_{2}\right)=\overline{Y}\) es posible computar la relación de insumos, la cual es simplemente la cantidad de un insumo dividido por el otro \(\frac{x_{2}}{x_{1}}\), como vemos representado por los gradientes de las líneas rosa y gris en el gráfico. Cualquier técnica de producción que use insumos \(x_{1}\) y \(x_{2}\) para alcanzar la producción \(\overline{Y}\) tendrá una relación de insumos específica a esa técnica en particular. Para cualquier punto dado \(\left(x_{1},x_{2}\right)\) en la isocuanta \(f\left(x_{1},x_{2}\right)=\overline{Y}\) uno puede calcular también la relación marginal de sustitución técnica \(\frac{-dx_{2}}{dx_{1}}\), que es la relación en la cual el insumo \(x_{1}\) puede ser intercambiado por el insumo \(x_{2}\) mientras se mantiene el nivel de producción en \(\overline{Y}\).

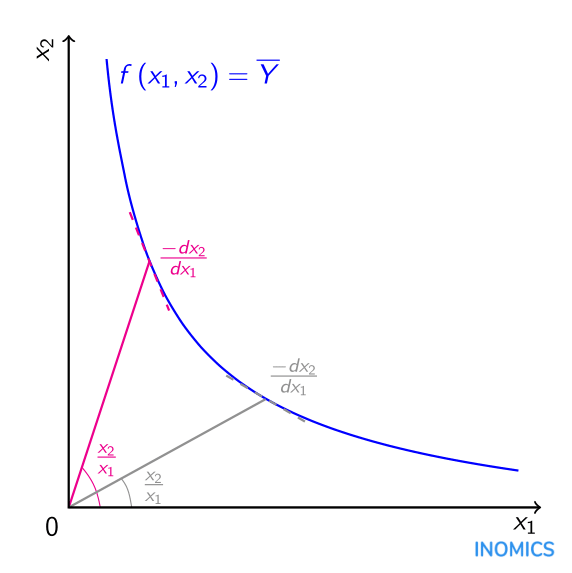
Esencialmente, la elasticidad de sustitución \(\sigma\) mide la facilidad con la cual poder moverse entre puntos a lo largo de una isocuanta. A la hora de moverse entre tales puntos, hay cambios tanto en la relación de insumos como en la relación marginal de sustitución técnica. La elasticidad de sustitución establece cambios proporcionados en la relación de insumos contra cambios proporcionados en la relación marginal de sustitución técnica, de tal manera que\[\sigma=\frac{\frac{\Delta\left(x_{2}/x_{1}\right)}{x_{2}/x_{1}}}{\frac{\Delta\left(-dx_{2}/dx_{1}\right)}{-dx_{2}/dx_{1}}}.\]

Un valor positivo de \(\sigma\) indica un cierto grado de sustituibilidad entre insumos de producción. En el extremo caso de sustitutos perfectos, la elasticidad de sustitución se aproxima a infinito \(\sigma\rightarrow\infty\). La electricidad de dos proveedores diferentes podría verse como un ejemplo de un sustituto perfecto: la electricidad hace el mismo trabajo de potenciar la producción, sin importar quién sea el proveedor. Por otro lado, un valor de \(\sigma=0\) indica justamente lo contrario: los insumos no pueden sustituirse el uno al otro, de hecho, son complementos perfectos, uno no puede ser empleado sin emplear también el otro. Por ejemplo, en la producción de coches, las ruedas requieren neumáticos; ninguno basta por su cuenta. De esta manera, las ruedas y los neumáticos son complementos perfectos. 

En general, la elasticidad de sustitución cambia en distintos puntos a lo largo de la isocuanta. por ejemplo, puede que sea más difícil cambiar máquinas por personas (low \(\sigma\)) cuando solo unas pocas personas están involucradas en la producción, mientras que es más fácil introducir máquinas (high \(\sigma\)) cuando siga habiendo suficientes personas para manejar las máquinas. No obstante, un caso especial es uno en el cual la elasticidad de sustitución está en un nivel constante para cualquier combinación de insumos de producción. Eso significa que, \(\sigma\) es el mismo valor en cualquier punto a lo largo de las isocuantas que representen la función de producción. En la práctica, ésto es un tanto irrealista, pero simplifica las matemáticas considerablemente, en particular para el modelamiento empírico, por lo que la asunción de Elasticidad de Sustitución Constante (CES) es popular entre economistas que estudian la producción. El ejemplo mejor conocido de una función de producción CES es la función de producción Cobb-Douglas .

La decisión sobre cómo organizar la producción depende tanto de la sustituibilidad de los insumos de producción (valor de \(\sigma\), forma de las isocuantas) como del coste relativo de los insumos en común, que puede ser representado por medio de líneas de isocoste. Por ejemplo, si una empresa energética produce electricidad tanto a través de una fuente medioambientalmente amigable (p.ej. viento) como de la quema de combustible de carbono, entonces la cantidad de cada insumo (viento o combustible de carbono) que la empresa asigne a la producción de electricidad será reducido a su relativo coste. Claramente, si la empresa sufre una mala reputación por causar daños al medioambiente, entonces el coste reputacional también se podría internalizar en el coste de producción, que aumentaría la probabilidad de que la empresa eligiese o incrementase el uso de la energía verde. En alternativa, el gobierno podría buscar una regulación del mercado de electricidad (ver los artículos sobre el fallo de mercado y externalidades positivas y negativas).

Lecturas adicionales

Para una aplicación de la elasticidad de la sustitución a la teoría de la economía medioambiental, mira el artículo de los economistas Daron Acemoglu, Philippe Aghion, Leonardo Bursztyn, y David Hemous, “The environment and directed technical change” (American Economic Review, 2012). Los autores comparan tecnologías ‘limpias’ y ‘sucias’ en un modelo de crecimiento sostenible, ofreciendo recomendaciones para distintos tipos de intervención del gobierno que dependen de la sustituibilidad de los insumos. 

Conviene saber

El concepto de la elasticidad de sustitución también se puede aplicar a la teoría de la demanda, para el análisis de curvas de indiferencia y la sustituibilidad de bienes y servicios en el consumo. El concepto tiene lugar a principios de los años 1930 cuando fue originalmente desarrollado de manera simultánea e independiente por los economistas John Hicks y Joan Robinson. ¡Irónicamente, uno podría argumentar que Hicks y Robinson eran buenos sustitutos, uno respecto al otro, en la producción de conocimiento económico, con un alto valor mutuo de \(\sigma\)! Sin embargo, desde la perspectiva del estudiante, un buen entendimiento de este concepto requiere algún esfuerzo. Como una vez dijo Thomas Edison, no hay sustituto para el trabajo duro.