Eine Cobb-Douglas-Produktionsfunktion modelliert die Beziehung zwischen Produktionsoutput und Produktionsinputs (Produktionsfaktoren). Sie wird verwendet, um die für eine effiziente Produktion nötigen Inputverhältnisse zu berechnen und so den technologischen Wandel in den Produktionsmethoden abzuschätzen. Die allgemeine Form einer Cobb-Douglas-Produktionsfunktion bei \(n\) Inputs lautet \[Y=f\left(x_{1},x_{2},...,x_{n}\right)=\gamma\prod^{n}_{i=1}x^{\alpha_{i}}_{i}\], wobei \(Y\) für den Output steht, \(x_{i}\) für Input \(i\), und \(\gamma\) sowie \(\alpha_{i}\) Parameter sind, die die Gesamteffizienz der Produktion und die Reaktionsfähigkeit des Outputs auf Änderungen der Inputmengen determinieren. Die Anwendung dieser Funktionsform zur Messung der Produktion geht auf den Mathematiker Charles Cobb und den Ökonomen Paul Douglas zurück. Sie nutzten die später nach ihnen benannte Cobb-Douglas- Produktionsfunktion, um die relative Bedeutung der beiden Inputfaktoren Arbeit und Kapital für den Produktionsoutput in den USA im Zeitraum von 1899 bis 1922 zu bestimmen. In ihrem ursprünglichen Modell begrenzten Cobb und Douglas die Parameter der Produktionselastizität \(\alpha_{1}\) und \(\alpha_{2}\) auf den Bereich \(\alpha_{i}\in\left(0,1\right)\) und setzen ihre Summe auf eins fest, was konstante Skalenerträge impliziert. Die Funktion lautet also: [Y=\gamma x^{\alpha_{1}}_{1}x^{1-\alpha_{1}}_{2}\], wobei \(x_{1}\) und \(x_{2}\) für Arbeit bzw. Kapital stehen. Bildet man den natürlichen Logarithmus für beide Seiten der Gleichung, so ergibt sich \[\ln{Y}=\ln{\gamma}+\alpha_{1}\ln{x_{1}}+\left(1-\alpha_{1}\right)\ln{x_{2}}\], sodass für Daten zum Output, Arbeit und Kapital die Parameter \(\gamma\) und \(\alpha_{1}\) mit Hilfe der Methode der kleinsten Quatdrate geschätzt werden können. Basierend auf ihren Daten finden Cobb und Douglas einen Wert von 0,75 für \(\alpha_{1}\), was bedeutet, dass im untersuchten Zeitraum Arbeit drei Viertel des Produktionsoutputs ausmachte (das verbleibende Viertel entfiel auf Kapital). Ihre Schätzung für den Effizienzparameter \(\gamma\) beträgt 1,01. Da 1,01 größer als 1 ist, bedeutet dieser Wert, dass diese Kombination von Arbeit und Kapital unbeobachtbare positive Auswirkungen auf die Produktion hat.

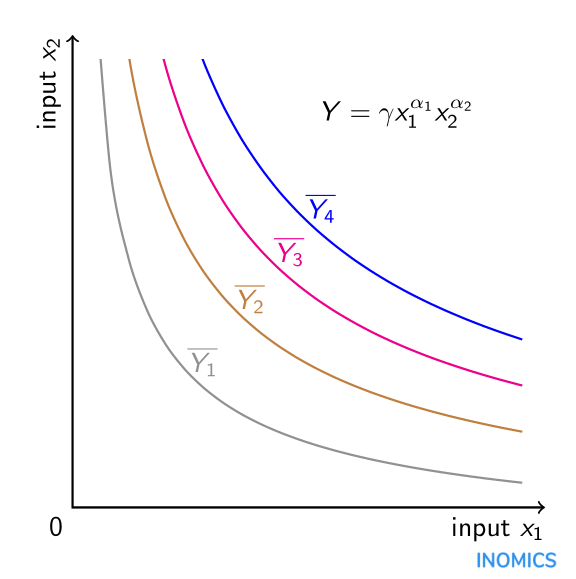
Eine Cobb-Douglas-Produktionsfunktion ist multiplikativer Natur in dem Sinne, dass  positive Werte für \(\alpha_{i}\) angenommen werden, was bedeutet, dass die Inputs Komplemente in der Produktion sind. Im Standardmodell von Arbeit und Kapital wird davon ausgegangen, dass eine Erhöhung der Kapitalmenge die Produktion nicht nur direkt steigert, sondern auch einen positiven indirekten Einfluss hat, da durch mehr Kapital auch die Produktivität der Arbeit gesteigert wird. Mathematisch bedeutet das, dass die Kreuzableitung des Produktionsoutputs \(Y\) nach Arbeit \(x_{1}\) und Kapital \(x_{2}\) positiv ist. Darüber hinaus sind aufgrund der Annahme, dass \(\alpha_{i}\in\left(0,1\right)\), die partiellen Ableitungen zweiter Ordnung des Produktionsoutputs nach Arbeit und Kapital beide negativ, was abnehmende Grenzerträge für jeden Input allein impliziert. Die Hinzufügung von entweder mehr Arbeit oder mehr Kapital (aber nicht von beidem) zum Produktionsprozess erhöht den Output zwar, allerdings mit abnehmender Rate. Außerdem ist die Substitutionselastizität zwischen den Inputs aufgrund der funktionalen Form konstant und gleich eins. Eine Cobb-Douglas-Produktionsfunktion mit zwei Inputs kann grafisch als Isoquante dargestellt werden: auf einer Isoquante finden sich alle Kombinationen beider Inputs, für die der Output konstant ist. In der Grafik sind vier Isoquanten für vier verschiedene (konstante) Outputniveaus dargestellt - \(\overline{Y_{1}}\), \(\overline{Y_{2}}\), \(\overline{Y_{3}}\) und \(\overline{Y_{4}}\). Je weiter die Isoquante vom Ursprung entfernt ist, desto höher ist der Output: \(\overline{Y_{4}}>\overline{Y_{3}}>\overline{Y_{2}}>\overline{Y_{1}}\). Welche genaue Kombination der Inputs \(x_{1}\) und \(x_{2}\) für die Produktion optimal ist, wird durch das dem Produzenten zur Verfügung stehende Budget sowie das Kostenverhältnis von Input \(x_{2}\) zu Input \(x_{1}\) bestimmt, das in Form einer Isokostenlinie in das Diagramm aufgenommen werden kann (lies dazu den Artikel zur Substitutionselastizität).

Cobb und Douglas räumten selbst ein, dass ihre besondere Form der Produktionsfunktion nicht auf soliden theoretischen Grundlagen beruht und auch nicht als Produktionsgesetz verstanden werden sollte; sie stellt lediglich eine statistische Annäherung an die beobachteten Beziehungen zwischen Produktionsinputs und Produktionsoutput dar. Dennoch sind die Eigenschaften der Funktion, die mathematische Berechnungen stark vereinfachen, für Ökonomen sehr praktisch und haben dazu geführt, dass die Cobb-Douglas-Produktionsfunktion im letzten Jahrhundert zu einem Standard in der mikroökonomischen Theorie wurde.

Zum Weiterlesen

Mehr zum Hintergrund und zu den wichtigsten Eigenschaften von Cobb-Douglas-Produktionsfunktionen, findest Du insbesondere in den Abschnitten 6, 7 und 8 des Originalartikels von Cobb und Douglas "A Theory of Production" (The American Economic Review, 1928).

Gut zu Wissen

Die Cobb-Douglas-Funktionsform wird nicht nur in der Produktionstheorie verwendet, sondern ist auch in der mikroökonomischen Konsumtheorie zum Standard geworden, wo sie als Nutzenfunktion angewendet wird, wobei dann \(Y\) zu \(U\) für Nutzen wird. Die \(x_{i}\) bilden dann die Konsumgüter ab und wenn die Nutzenfunktion unter einer Budgetbeschränkung maximiert wird, geben die Werte für \(\alpha_{i}\) an, wie das Individuum das Budget optimal auf die Güter verteilen wird.

​