Una funzione di produzione Cobb-Douglas modella la relazione tra l'output di produzione e gli input di produzione (fattori). È usata per calcolare i rapporti tra gli input per una produzione efficiente e per stimare il cambiamento tecnologico nei metodi di produzione. La forma generale di una funzione di produzione di Cobb-Douglas per un insieme di \(n\) fattori è \[Y=f\left(x_{1},x_{2},...,x_{n}\right)=\gamma\prod^{n}_{i=1}x^{\alpha_{i}}_{i}\] dove \(Y\) sta per la produzione, \(x_{i}\) per gli input \(i\), e \(\gamma\) e \(\alpha_{i}\) sono parametri che determinano l'efficienza complessiva della produzione e la reattività della produzione ai cambiamenti nelle quantità degli input. L'applicazione di questa forma funzionale nella misurazione della produzione è dovuta al matematico Charles Cobb e all'economista Paul Douglas, che la utilizzarono per considerare l'importanza relativa dei due fattori produttivi, lavoro e capitale, nella produzione manifatturiera negli USA nel periodo 1899-1922. Nel loro modello originale, Cobb e Douglas restringono i parametri di elasticità della produzione \(\alpha_{1}\) e \(\alpha_{2}\) all'intervallo \(\alpha_{i}\in\left(0,1\right)\) e alla somma di uno, che implica rendimenti di scala costanti. La funzione è quindi \[Y=\gamma x^{\alpha_{1}}_{1}x^{1-\alpha_{1}}_{2}\] dove \(x_{1}\) e \(x_{2}\) stanno rispettivamente per lavoro e capitale. Prendendo il logaritmo naturale di entrambi i lati dell'equazione otteniamo \[\ln{Y}=\ln{\gamma}+\alpha_{1}\ln{x_{1}}+\left(1-\alpha_{1}\right)\ln{x_{2}}\] in modo tale che per i dati su produzione, lavoro e capitale, i parametri \(\gamma\) e \(\alpha_{1}\) possono essere stimati usando il metodo dei minimi quadrati ordinari. Sulla base dei loro dati, Cobb e Douglas trovano un valore di 0,75 per \(\alpha_{1}\), che implica che il lavoro rappresenta tre quarti del valore della produzione manifatturiera statunitense (il capitale rappresenta il quarto rimanente) nel periodo studiato. La loro stima per il parametro di efficienza \(\gamma\) è 1,01, che, essendo maggiore di 1, riflette gli effetti positivi delle forze non osservabili sulla produzione attraverso la combinazione di lavoro e capitale.

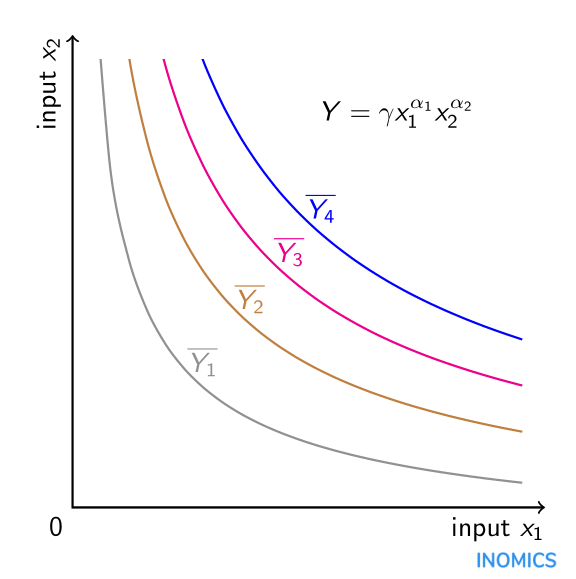
La natura moltiplicativa di una funzione di produzione Cobb-Douglas, assumendo valori positivi per \(\alpha_{i}\), significa che gli input sono complementari nella produzione. Nel modello standard di lavoro e capitale, l'aumento della quantità di capitale aumenta la produzione non solo direttamente, ma anche indirettamente attraverso il suo impatto sulla produttività del lavoro. Matematicamente, la derivata incrociata dell'output di produzione \(Y\) rispetto al lavoro \(x_{1}\) e al capitale \(x_{2}\) è positiva. Inoltre, a causa dell'assunzione che \(\alpha_{i}\in\left(0,1\right)\), le derivate parziali del secondo ordine della produzione rispetto al lavoro e rispetto al capitale sono entrambe negative, implicando rendimenti marginali decrescenti per ogni singolo input. Aggiungere semplicemente più lavoro o più capitale (ma non entrambi) al processo di produzione aumenta la produzione, anche se ad un tasso decrescente. Inoltre, l'elasticità di sostituzione tra gli input è costante e uguale a uno a causa della forma funzionale. Una funzione di produzione Cobb-Douglas a due fattori può essere rappresentata graficamente sotto forma di isoquanti: combinazioni di entrambi i fattori per cui l'output è costante. Ci sono quattro di questi isoquanti nel grafico sottostante per i livelli di output (costante) \(\overline{Y_{1}}\), \(\overline{Y_{2}}\), \(\overline{Y_{3}}\) e \(\overline{Y_{4}}\). Più l'isoquanto è lontano dall'origine, maggiore è il livello di output \(\overline{Y_{4}}>\overline{Y_{3}}>\overline{Y_{2}}>\overline{Y_{1}}\). Quale precisa combinazione degli input \(x_{1}\) e \(x_{2}\) sia ottimale per la produzione è determinata dal budget a disposizione del produttore così come dal rapporto di costo dell'input \(x_{2}\) rispetto all’input \(x_{1}\) che può essere incluso nel grafico nella forma di una retta di isocosto (vedere l'articolo sull'elasticità di sostituzione).

Gli stessi Cobb e Douglas riconobbero che la loro funzione di produzione non poggia su solide basi teoriche, né dovrebbe essere intesa come una legge di produzione: essa rappresenta semplicemente un'approssimazione statistica delle relazioni osservate tra input e output di produzione. Tuttavia, le sue semplici proprietà matematiche sono attraenti per gli economisti, e l'hanno portata a diventare uno standard nella teoria microeconomica nell'ultimo secolo.

Altre letture:

Per il background e una panoramica delle principali proprietà delle funzioni di produzione Cobb-Douglas, vedete in particolare le sezioni 6, 7 e 8 dell'articolo originale di Cobb e Douglas, “A Theory of Production” (The American Economic Review, 1928).

Buono a sapersi:

La forma funzionale di Cobb-Douglas non è solo usata nella teoria della produzione, ma è anche diventata uno standard nella teoria microeconomica del consumo, dove è applicata come funzione di utilità, in cui \(Y\) diventa \(U\) per l'utilità. I \(x_{i}\) rappresentano quindi i beni di consumo e, quando la funzione di utilità è massimizzata soggetta a un vincolo di bilancio, i valori di \(\alpha_{i}\) indicano come l'individuo distribuirà in modo ottimale il bilancio tra i beni.