Una función de producción Cobb-Douglas modela la relación entre la producción y los inputs (factores) de producción. Se utiliza para calcular las relaciones de un input con otro, para una producción eficiente y para estimar cambios tecnológicos en los métodos de producción. La forma general de una función de producción para un conjunto de \(n\) factores es \[Y=f\left(x_{1},x_{2},...,x_{n}\right)=\gamma\prod^{n}_{i=1}x^{\alpha_{i}}_{i}\] donde \(Y\) representa la producción, \(x_{i}\) los factores \(i\), y tanto \(\gamma\) como \(\alpha_{i}\) son parámetros que determinan la eficiencia general de la producción y la sensibilidad de la producción ante cambios en la cantidad de los factores. La forma en que se aplica esta función como medida de la producción se debe al matemático Charles Cobb y al economista Paul Douglas, quienes la usaron para considerar la importancia relativa de los dos factores de producción, trabajo y capital, en la producción manufacturera de EE.UU entre los años 1899 y 1922. En su modelo original, Cobb y Douglas limitan los parámetros de la elasticidad de la producción \(\alpha_{1}\) y \(\alpha_{2}\) al intervalo \(\alpha_{i}\in\left(0,1\right)\) teniendo que sumar uno en conjunto, lo cual implica rendimientos de escala constantes. La función es entonces \[Y=\gamma x^{\alpha_{1}}_{1}x^{1-\alpha_{1}}_{2}\] donde \(x_{1}\) y \(x_{2}\) representan trabajo y capital respectivamente. Tomando el logaritmo neperiano de ambas partes de la ecuación obtenemos \[\ln{Y}=\ln{\gamma}+\alpha_{1}\ln{x_{1}}+\left(1-\alpha_{1}\right)\ln{x_{2}}\] de manera que para los datos de producción, trabajo y capital, los parámetros \(\gamma\) y \(\alpha_{1}\) puedan ser estimados mediante Mínimos Cuadrados Ordinarios. En base a sus datos, Cobb y Douglas encuentran un valor de 0.75 para \(\alpha_{1}\), lo cual implica que el trabajo representaba tres cuartos del valor de la producción manufacturera en EE.UU (donde el capital representaba el cuarto restante) a lo largo del periodo estudiado. Su estimación para el parámetro de eficiencia \(\gamma\) es 1.01, el cual, dado que es mayor que 1, refleja los efectos positivos de determinadas fuerzas inobservables sobre la producción mediante la combinación de trabajo y capital.

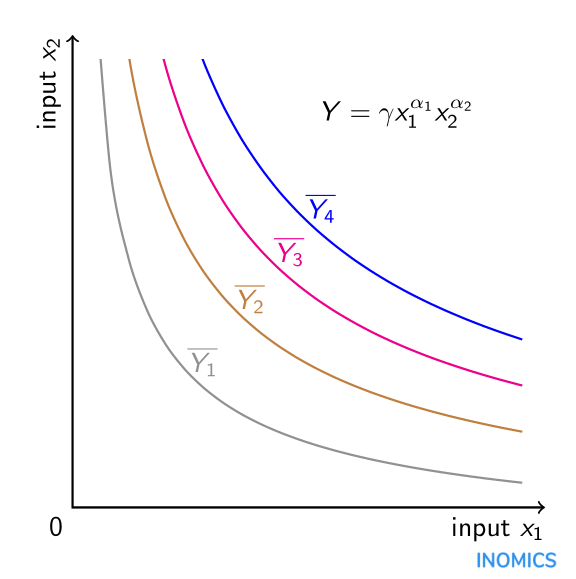
La naturaleza multiplicativa de una función de producción Cobb-Douglas, asumiendo valores positivos para \(\alpha_{i}\), significa que los inputs son complementos en la producción. En el modelo estándar del trabajo y el capital, aumentar la cantidad de capital incrementa la producción no solo directamente, sino también indirectamente mediante su impacto en la productividad del trabajo. Matemáticamente, la derivada cruzada parcial de la producción \(Y\) con respecto al trabajo \(x_{1}\) y al capital \(x_{2}\) es positiva. Además, debido a la hipótesis de que \(\alpha_{i}\in\left(0,1\right)\), las derivadas parciales de segundo orden de la producción con respecto al trabajo y con respecto al capital son ambas negativas, implicando rendimientos marginales decrecientes para cada factor. Simplemente añadiendo más trabajo o más capital (pero no ambos) al proceso de producción aumenta la producción, aunque a una tasa decreciente. Además, la elasticidad de sustitución entre los factores es constante e igual a uno debido a la función. Una función de producción Cobb-Douglas de dos factores se puede representar gráficamente en forma de isocuantas: combinaciones de ambos factores para los cuales la producción es constante. Existen cuatro isocuantas en el gráfico de abajo para los niveles (constantes) de producción \(\overline{Y_{1}}\), \(\overline{Y_{2}}\), \(\overline{Y_{3}}\) y \(\overline{Y_{4}}\). Cuanto más lejos esté la isocuanta del origen, mayor será el nivel de producción \(\overline{Y_{4}}>\overline{Y_{3}}>\overline{Y_{2}}>\overline{Y_{1}}\). La combinación óptima de los factores \(x_{1}\) y \(x_{2}\) para la producción se determina por los recursos que el productor tiene disponibles, al igual que por la relación de costes del factor \(x_{2}\) al factor \(x_{1}\) que se puede incluir en el gráfico en forma de una línea de isocoste (ver el artículo sobre elasticidad de sustitución).

Lecturas adicionales:

Para contextualizarse y tener una perspectiva general de las principales propiedades de las funciones de producción Cobb-Douglas, consulta en particular las secciones 6, 7 y 8 del artículo original de Cobb y Douglas, “A Theory of Production” (The American Economic Review, 1928).

Good to know:

La forma funcional de Cobb-Douglas no se utiliza solamente en la teoría de producción, sino que también se ha convertido en la norma dentro de la teoría microeconómica del consumidor, donde se aplica como una función de utilidad, donde \(Y\) pasa a ser \(U\) para la utilidad. El factor \(x_{i}\) representa entonces niveles de consumo y, cuando la función de utilidad se maximiza sujeta a una restricción presupuestaria, los valores de \(\alpha_{i}\) indican la manera en que el individuo distribuirá óptimamente los recursos entre los niveles. 

​