Le Duopole de Bertrand (ou modèle de compétition de Bertrand) est un modèle de concurrence dans lequel deux ou plusieurs entreprises produisent un bien homogène et se font concurrence sur les prix. En théorie, cette concurrence sur les prix, à condition que les biens soient des substituts parfaits, aboutit à ce que les entreprises vendent leurs biens au coût marginal et ne réalisent aucun bénéfice. Ce résultat est également appelé le “paradoxe de Bertrand”, du nom de l'économiste Joseph Bertrand (1822-1900).

Les hypothèses du modèle

Le Duopole de Bertrand est une concurrence par les prix sur un marché oligopolistique dans lequel deux entreprises ou plus produisent un bien homogène. Examinons les principales hypothèses du modèle :

• Bien homogène : Les biens qui sont produits et vendus par les entreprises concurrentes sont totalement identiques aux yeux des consommateurs. Les consommateurs n'ont aucune préférence pour l'une ou l'autre des entreprises et achètent donc à l'entreprise qui offre le bien au prix le plus bas.
• La concurrence par les prix : Contrairement à la concurrence de Cournot ou de Stackelberg, les entreprises ne se font pas concurrence sur les quantités, mais sur les prix. Cela signifie que chaque entreprise fixe le prix de son produit dans le but de maximiser son propre profit (et bien sûr en tenant compte des prix fixés par les entreprises concurrentes).

Un exemple simple du Duopole de Bertrand est le marché de l'essence. Les stations-service annoncent le prix du litre et les consommateurs (conducteurs) décident dans quelle station-service ils font le plein de leur voiture. L'essence étant un bien homogène, la plupart des consommateurs opteront pour la station-service dont le prix est le plus bas.

L'équilibre de Bertrand-Nash dans l’équilibre de Nash

Les entreprises fixent leurs prix à un niveau égal aux coûts marginaux et ne font aucun profit. Essayons de comprendre pourquoi cela se produit. Supposons que deux entreprises produisent un bien homogène à des coûts marginaux constants notés \(c\) et se font concurrence en fixant simultanément leurs prix. Les consommateurs achètent à l'entreprise qui pratique le prix le plus bas, car ils perçoivent les biens vendus par les deux entreprises comme de parfaits substituts. Nous supposerons que la demande est répartie également si les entreprises pratiquent le même prix.

Le bénéfice de l'entreprise \(i\) est donné par \(\pi_{i}=(p_{i}-c)D_{i}(p_{i},p_{j})\) s'il n'y a pas de coûts fixes, où \(D_{i}(p_{i},p_{j})\) est la demande à laquelle fait face l'entreprise \(i\) si l'entreprise \(i\) applique le prix \(p_{i}\) et l'entreprise \(j\) applique le prix \(p_{j}\). La demande \(D_{i}(p_{i},p_{j})\) à laquelle fait face l'entreprise \(i\) dépend des prix des deux entreprises :

1. Si l'entreprise \(i\) facture un prix plus élevé que l'entreprise \(j\) (\(p_{i}>p_{j}\)), tous les consommateurs achètent à l'entreprise \(j\), l'entreprise \(i\) n'a pas de demande et réalise un profit de zéro.

2. Si l'entreprise \(j\) pratique un prix plus élevé que l'entreprise \(i\) (\(p_{j}>p_{i}\)), tous les consommateurs achètent à l'entreprise \(i\) et l'entreprise \(i\) réalise un bénéfice de \(\pi_{i}=(p_{i}-c)D(p_{i})\).

3. Si les entreprises \(i\) et \(j\) pratiquent le même prix (\(p_{i}=p_{j}\)), la demande est répartie également et l'entreprise \(i\) réalise un bénéfice de \(\pi_{i}=(p_{i}-c)\frac{1}{2}D(p_{i})\).

Alors pourquoi les entreprises fixent-elles leurs prix aux coûts marginaux à l'équilibre ? Pour bien le comprendre, supposons que deux entreprises, appelons-les Airbus (entreprise \(A\)) et Boeing (entreprise \(B\)) produisent le même avion de ligne à des coûts marginaux égaux à 10 millions de dollars américains. Les clients achètent à l'entreprise qui pratique le prix le plus bas. Supposons que Boeing impose un prix supérieur aux coûts marginaux, par exemple 50 millions par avion (\(p_{B}=50\)) : Airbus a maintenant trois options. Elle peut demander le même prix, un prix plus élevé ou un prix plus bas. Il est clair qu'un prix plus élevé n'a pas beaucoup de sens, car tous les clients resteraient avec l’entreprise \(B\). En fixant le même prix, les deux entreprises se partagent la demande de manière égale et chacune réalise un bénéfice de \(\pi_{i}=\frac{(p-c)D(p_{i})}{2}=20D(p)\). Si l'entreprise \(A\) pratique un prix inférieur à \(p_{B}\), le prix le plus élevé qu'elle peut pratiquer pour obtenir tous les clients est un prix légèrement inférieur à celui de l'entreprise \(B\), c'est-à-dire 49,99 millions de dollars américains. Airbus obtient alors la totalité de la demande et réalise un bénéfice de \(\pi_{A}=39.99D(p_{A})\). Ce bénéfice est supérieur au bénéfice partagé à prix égaux si l'entreprise \(A\) facture un prix à peine inférieur à celui de l'entreprise \(B\). Mais bien sûr, si Airbus pratique un prix légèrement inférieur à celui de Boeing, Boeing n'a pas de demande et réalise un bénéfice nul. En facturant un prix légèrement inférieur à celui d'Airbus, elle peut obtenir la totalité de la demande et réaliser un profit positif. En d'autres termes, chaque entreprise veut casser le prix de son rival pour obtenir la totalité de la demande du marché. L'incitation à casser le prix du rival ne disparaît que lorsqu’une diminution supplémentaire du prix n'augmente plus les bénéfices, ce qui se produit lorsque le prix est égal aux coûts marginaux. Si le concurrent fixe son prix aux coûts marginaux, il n'est pas logique que l'autre entreprise fixe un prix plus élevé ou plus bas ; à un prix plus élevé, l'entreprise n'a pas de clients et, à un prix inférieur aux coûts marginaux, l'entreprise subit une perte. Ce résultat est indépendant du nombre d'entreprises, ce qui signifie que même s'il n'y a que deux entreprises sur le marché, les prix sont égaux aux coûts marginaux et les profits sont nuls (comme dans la concurrence parfaite).

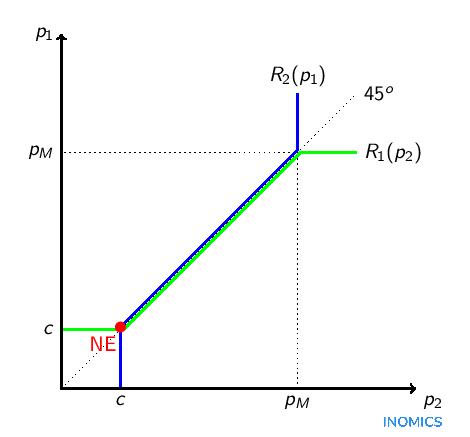
Examinons les fonctions de meilleure réponse des entreprises symétriques dans un jeu de Bertrand, comme le montre la figure ci-dessous. La ligne bleue représente la fonction de meilleure réponse de l'entreprise 2 pour un prix donné \(p_{1}\) et la ligne verte la fonction de meilleure réponse de l'entreprise \(1\). \(p_{M}\) désigne le prix de monopole. Si vous regardez attentivement, vous verrez que la ligne verte est légèrement inférieure à la ligne de 45 degrés - les pointillés le long de cette ligne indiquant que les deux entreprises pratiquent le même prix - si le prix de l'entreprise 2 est supérieur aux coûts marginaux et inférieur au prix de monopole. Pour tout prix pratiqué par l'entreprise 2 dans cet intervalle, l'entreprise 1 pratiquera un prix légèrement inférieur. Il en va de même pour l'entreprise 2, bien sûr. Les fonctions de meilleure réponse sont en pente ascendante parce qu'à un prix plus élevé du concurrent, chaque entreprise facturera un prix plus élevé. L'intersection des deux lignes (le point rouge) représente l'unique équilibre de Nash du jeu. Il n'y a qu'un seul point où les entreprises jouent une meilleure réponse mutuelle et aucune entreprise n'a intérêt à changer de décision étant donné le prix choisi par le concurrent. Comme on peut le voir sur la figure, c'est à ce point que le prix est égal aux coûts marginaux.

En savoir plus

Lorsque les entreprises ne sont pas aussi efficaces les unes que les autres - c'est-à-dire que l'une d'entre elles a des coûts marginaux inférieurs à ceux des autres entreprises - l'entreprise ayant le coût marginal le plus bas obtiendra la totalité de la demande et réalisera un profit positif. Spulber détaille dans l’ouvrage "Bertrand competition when rivals' costs are unknown" (The Journal of Industrial Economics, 1995) que les deux entreprises fixent leurs prix au-dessus des coûts marginaux et obtiennent des bénéfices positifs si elles ne connaissent pas la fonction de coût du concurrent.

Bon à savoir

Dans les marchés du monde réel, les entreprises réalisent généralement des profits positifs. Comment cela se fait-il ? Tout d'abord, les entreprises offrent rarement des biens parfaitement homogènes. Même si le bien physique que deux entreprises vendent est le même, les biens produits ou vendus par des entreprises différentes ne sont pas perçus comme identiques (substituts parfaits) par les consommateurs. Les consommateurs peuvent préférer acheter le bien d’une entreprise particulière pour diverses raisons, par exemple parce que l'emplacement du magasin est plus pratique ou que différents services sont proposés avec le bien. Deuxièmement, dans le jeu classique de Bertrand, les entreprises n'interagissent qu'une seule fois. Sur les marchés du monde réel, les mêmes entreprises se font concurrence jour après jour et peuvent coopérer pour maintenir les prix au-dessus des coûts marginaux. Troisièmement, les entreprises peuvent être soumises à des contraintes de capacité, ce qui signifie qu'elles peuvent ne pas être en mesure de servir l'ensemble du marché. Par conséquent, l'entreprise qui pratique le prix le plus élevé ne perdra pas tous ses clients au profit de son concurrent et réalisera un bénéfice positif même si elle pratique un prix supérieur aux coûts marginaux.