Economics Terms A-Z
La Boîte d'Edgeworth
Read a summary or generate practice questions using the INOMICS AI tool
Une boîte d'Edgeworth (du nom du philosophe et économiste irlandais Francis Ysidro Edgeworth, 1881) est une représentation bidimensionnelle d'une économie simple et fermée composée de deux individus et de deux articles (ou ressources) dont l'offre est limitée. Toute allocation possible des biens entre les individus est représentée par un point dans la boîte ; les préférences des individus pour les biens sont représentées par des courbes d'indifférence.
L'avantage de représenter une économie de cette manière est de permettre la comparaison de différentes allocations et de déterminer leur efficacité relative. Considérons l'exemple suivant d'une économie comportant deux individus, Adam et Ève, et deux articles, des dattes et du lait. Le nombre total de dattes dans l'économie est représenté par la longueur horizontale de la boîte ; la quantité totale de lait est mesurée par sa longueur verticale. Dans le coin inférieur gauche \(o\), Adam ne possède rien tandis qu'Ève possède/consomme toutes les dattes et le lait. Dans le coin opposé, supérieur droit, \(o'\), Adam possède tout tandis qu'Ève ne possède rien. Les courbes d'indifférence \(A_{1}\), \(A_{2}\) et \(A_{3}\) représentent les préférences d'Adam pour les dattes et le lait, avec une utilité plus élevée sur \(A_{3}\) que sur \(A_{1}\) ; de manière analogue, les courbes d'indifférence \(E_{1}\), \(E_{2}\) et \(E_{3}\) représentent les préférences d'Eve pour les dattes et le lait, avec une utilité plus élevée sur \(E_{3}\) que sur \(E_{1}\).
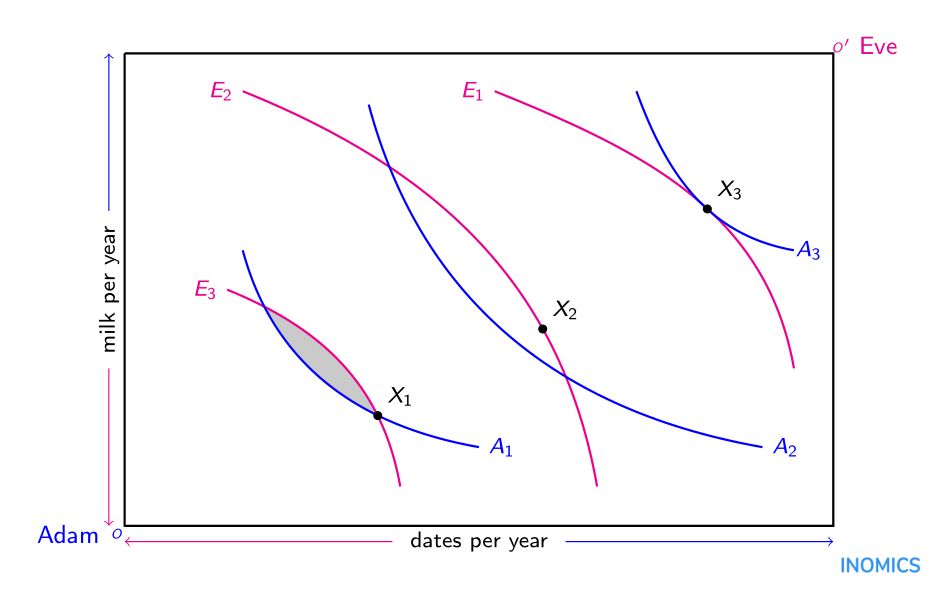
Les points \(X_{1}\), \(X_{2}\) et \(X_{3}\) montrent trois répartitions différentes des dattes et du lait entre Adam et Ève. À \(X_{1}\), Adam est sur sa courbe d'indifférence \(A_{1}\) tandis qu'Ève est sur sa courbe d'indifférence \(E_{3}\). Cependant, cette allocation n'est pas efficiente conformément au principe de Pareto, car Adam et Ève pourraient être mieux lotis (obtenir une utilité supérieure) avec une autre allocation située n'importe où dans la zone grisée délimitée par les courbes d'indifférence \(A_{1}\) et \(E_{3}\). En revanche, l'allocation à \(X_{3}\) où les courbes d'indifférence \(A_{3}\) et \(E_{1}\) se touchent tangentiellement est efficiente conformément au principe de Pareto parce que ni Adam ni Ève ne peuvent obtenir une utilité supérieure par une allocation différente sans réduire l'utilité de l'autre. Notons cependant qu'à \(X_{3}\), Adam a beaucoup plus de dattes et de lait qu'Ève, alors que l'inverse est aussi vrai à \(X_{1}\). Le fait que \(X_{3}\) soit une allocation efficace ne dit rien sur son équité. En effet, un point plus proche du milieu de la boîte d'Edgeworth, comme l'allocation à \(X_{2}\), peut être considéré comme plus équitable que \(X_{1}\) ou \(X_{3}\) puisque les dattes et le lait sont répartis de manière plus égale entre Adam et Ève. Pourtant, par un raisonnement similaire à celui de \(X_{1}\), l'allocation de \(X_{2}\) n'est pas efficiente conformément au principe de Pareto ; elle peut être améliorée sans nuire à aucun des individus de l'économie. L'ensemble des allocations efficientes conformément au principe de Pareto peut être révélé dans une boîte d'Edgeworth sous la forme d'une "courbe des contrats” qui s'étend entre les coins d'origine (\(o\) et \(o'\)) en passant par tous les points où les courbes d'indifférence se rencontrent tangentiellement. Notons que si chaque allocation sur une telle courbe est efficace, elle n'est pas nécessairement équitable.
En savoir plus
Le compromis classique entre l'efficacité et l'équité a longtemps été un point de discorde majeur en économie politique. Koichi Tadenuma utilise les boîtes d'Edgeworth pour montrer comment le fait de privilégier l'équité par rapport à l'efficacité peut parfois donner lieu à des résultats socialement plus souhaitables. Pour plus d’informations, nous vous conseillons de consulter son article "Efficiency First or Equity First ? Two Principles and Rationality of Social Choice" (Journal of Economic Theory, 2002).
Bon à savoir
Les boîtes d'Edgeworth sont un outil utile pour étudier le commerce de deux ressources limitées entre deux économies distinctes. Il est possible de démontrer que l'utilité des deux économies augmente, car le commerce permet aux économies de réaliser des allocations de ressources plus efficaces et plus équitables que dans un état d'autarcie. Les partisans du libre-échange peuvent également faire valoir que des boîtes d'Edgeworth plus grandes peuvent être obtenues par l'échange, car l'exploitation de l'avantage comparatif de chaque économie en matière de production devrait conduire à une plus grande disponibilité globale des biens et des services.
-
- PhD Program, Program, Postgraduate Scholarship
- Posted 1 week ago
PhD Program in Management - 11 Fully Funded Scholarships
at Luiss Guido Carli University of Rome in Rome, Italie
-
- Conférence
- Posted 3 weeks ago
Industrial Policies in a Globalized and Financialized World
Between 7 May and 8 May -
- Professional Training Course, Supplementary Course, Online Course
- (Online)
- Posted 1 week ago
Maximising the Potential of Stata’s new Python Capabilities - Live Online Course
Starts 9 Apr at TStat Training












