Las derivadas de las funciones se computan usando cálculos diferenciales y son extensamente aplicadas en la modelización económica para medir los efectos y los tipos de cambio en las variables económicas, al igual que para determinar los valores máximos y mínimos de las funciones. 

Considera la siguiente función de coste de producción para un bien\[C\left(q\right)=k+aq^2\] donde \(k\) es un coste fijo, \(q\) el número de unidades producidas y \(a\) un parámetro de coste variable. \(C\left(q\right)\) representa el coste de producción total para \(q\) unidades del producto. A la hora de tomar la decisión sobre cuánta cantidad del bien producir, una empresa maximizadora de beneficios se interesará por el coste de producir la última unidad del producto (coste marginal), con el objetivo de igualar éste al ingreso adicional que resulta de vender esa unidad (ingreso marginal). Supongamos que el ingreso (total) de vender este producto es simplemente el precio unitario \(p\) multiplicado por la cantidad vendida\[R\left(q\right)=pq.\] Entonces el beneficio \(\pi\) será el ingreso menos el coste\[\pi\left(q\right)=R\left(q\right)-C\left(q\right).\]

El beneficio máximo se encuentra tomando la primera derivada de la función del beneficio e igualándola a cero\[\begin{aligned} \frac{\partial\pi\left(q\right)}{\partial q}=\frac{\partial R\left(q\right)}{\partial q}-\frac{\partial C\left(q\right)}{\partial q}&=0\\ \Leftrightarrow\ \ \ \frac{\partial R\left(q\right)}{\partial q}&=\frac{\partial C\left(q\right)}{\partial q}\\ \Leftrightarrow\ \ \ p&=2aq\\ \Rightarrow\ \ \ q^{*}&=\frac{p}{2a}.\end{aligned}\] Dado que la primera derivada de la función del beneficio es cero en este punto, los beneficios no están ni creciendo ni disminuyendo. Se puede verificar que el punto es un máximo (y no un mínimo) tomando la segunda derivada de la función del beneficio\[\begin{aligned} \frac{\partial^{2}\pi\left(q\right)}{\partial q^{2}}&=\frac{\partial^{2}\left(pq-\left(k+aq^{2}\right)\right)}{\partial q^{2}}\\ &=-2a,\end{aligned}\] la cual es negativa para una \(a\) positiva, i.e. el gradiente de la función del beneficio es decreciente en \(q\). Ésto significa que los beneficios siguen creciendo en \(q<q^{*}\) aunque disminuyendo en \(q>q^{*}\) y por lo tanto los beneficios se encuentran al máximo en \(q=q^{*}\).

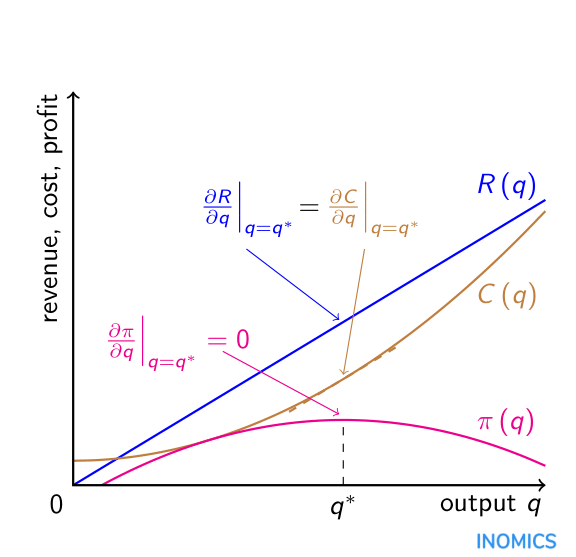
Este ejemplo es representado en el siguiente gráfico donde se muestra cómo los beneficios \(\pi\) están maximizados en el punto \(q=q^{*}\) donde la primera derivada de la función del ingreso (ingreso marginal) \(\frac{\partial R}{\partial q}\) es igual a la primera derivada de la función del coste (coste marginal) \(\frac{\partial C}{\partial q}\).

El ejemplo de arriba implica relaciones simples, directas y parciales entre la cantidad del producto \(q\) y el ingreso/ coste/ beneficio. En la mayoría de las situaciones del mundo real el ingreso y el coste también dependerán de otras variables, por ejemplo, las fuerzas de ventas \(e\) y el gasto en marketing \(m\) para el ingreso, y el precio de las materias primas \(r\) y los salarios \(w\) para el coste. En la medida en que estas otras variables interactúan con la cantidad de producción puede que sea necesario calcular las derivadas totales de las funciones del ingreso y el coste con respecto a \(q\) para determinar el nivel óptimo de producción,\[\begin{aligned} \frac{dR\left(q,e\left(q\right),m\left(q\right)\right)}{dq}&=\frac{\partial R}{\partial q}+\frac{\partial R}{\partial e}\frac{de}{dq}+\frac{\partial R}{\partial m}\frac{dm}{dq};\\ \frac{dC\left(q,r\left(q\right),w\left(q\right)\right)}{dq}&=\frac{\partial C}{\partial q}+\frac{\partial C}{\partial r}\frac{dr}{dq}+\frac{\partial C}{\partial w}\frac{dw}{dq}.\end{aligned}\] Calcular estas derivadas totales toma en cuenta cualquier efecto indirecto en el ingreso y el coste por cambiar la cantidad de producción que resultan de las diferencias potenciales en las fuerzas de ventas, el gasto en marketing, el precio de las materias primas y los salarios provocadas por el cambio en la cantidad de producción.  

Lecturas adicionales

Hal Varian ofrece una introducción sencilla para los economistas sobre cómo calcular derivadas de funciones, tanto totales como parciales, en el anexo matemático de su popular libro de texto Intermediate Microeconomics: A Modern Approach (see sections A10 to A13 of the ninth edition).

Conviene saber

En la mayoría de los casos, cuando los economistas calculan derivadas de una función están llevando a cabo un análisis ceteris-paribus. Tomar la derivada parcial de una función \(y=f\left(x_{1},\cdot\right)\) con respecto a \(x_{1}\) viene a ser estimar el efecto de \(x_{1}\) sobre \(y\) asumiendo que todo el resto se mantiene igual. 

​