Bertrand competition is a model of competition in which two or more firms produce a homogenous good and compete in prices. Theoretically, this competition in prices, providing the goods are perfect substitutes, ends with the firms selling their goods at marginal costs and thus making zero profits. The result is also called the Bertrand paradox, named after the economist Joseph Bertrand (1822–1900).

Model assumptions

Bertrand competition is price competition in an oligopolistic market in which two or more firms produce a homogeneous good. Let's have a quick look at the main assumptions of the model:

• Homogeneous good: The goods that are being produced and sold by competing firms are completely identical in the eyes of the consumers. Consumers have no preference for either of the firms and therefore buy from the firm offering the good at a lower price.
• Competition in prices: In contrast to Cournot or Stackelberg competition, firms do not compete in quantities but in prices. This means that each firm sets the price for its product with the aim to maximize its own profit (and of course taking into account the prices set by competing firms).

A standard example for Bertrand competition is the market for gasoline. Petrol stations announce the price per liter and the consumers (drivers) decide at which petrol station they refuel their car. As petrol is a homogeneous good, most of the consumers will opt for the petrol station with the lowest price (of course, we must assume the petrol stations in question are located next to each other; otherwise convenience of location can cause these goods to be heterogeneous).

In the unique Nash equilibrium of the Bertrand competition model, firms set their prices equal to marginal costs and make no profit. Let us try to understand why this happens. Suppose there are two firms that produce a homogeneous good at constant marginal costs denoted by \(c\) and compete by simultaneously setting prices. Consumers buy from the firm charging the lower price, because they perceive the goods sold by the two firms as perfect substitutes. We will assume that the demand is split equally if firms charge the same price.

The profit of firm \(i\) is given by \(\pi_{i}=(p_{i}-c)D_{i}(p_{i},p_{j})\) if there are no fixed costs, where \(D_{i}(p_{i},p_{j})\) is the demand faced by firm \(i\) if firm \(i\) charges price \(p_{i}\) and firm \(j\) charges price \(p_{j}\). The demand \(D_{i}(p_{i},p_{j})\) faced by firm \(i\) depends on the prices of both firms:

1. If firm \(i\) charges a higher price than firm \(j\) (\(p_{i}>p_{j}\)) all consumers buy from firm \(j\), firm \(i\) has no demand and makes a profit of zero.
2. If firm \(j\) charges a higher price then firm \(i\) (\(p_{j}>p_{i}\)) all consumers buy from firm \(i\) and firm \(i\) makes a profit of \(\pi_{i}=(p_{i}-c)D(p_{i})\).
3. If firms \(i\) and \(j\) charge the same price (\(p_{i}=p_{j}\)) demand is split equally and firm \(i\) makes a profit of \(\pi_{i}=(p_{i}-c)\frac{1}{2}D(p_{i})\).

So why will firms price at marginal costs in equilibrium? To understand this, suppose that two firms, let us call them Airbus (firm \(A\)) and Boeing (firm \(B\)) produce the same passenger plane at marginal costs equal to 10 million US Dollars. Customers buy from the firm charging the lower price (in this case, customers would include militaries, airlines, or airplane leasing companies that then lease airplanes to airlines). Let us say that Boeing charges a price above marginal costs, for example 50 million per plane (\(p_{B}=50\)). Now Airbus has three options. It can charge the same price, a higher price or a lower price.

• Clearly, a higher price does not make much sense, because all customers would remain with firm \(B\).
• Setting the same price means that the two firms share the demand equally and each firm makes a profit of \(\pi_{i}=\frac{(p-c)D(p_{i})}{2}=20D(p)\).
• If firm \(A\) charges a price below \(p_{B}\), the highest price it can charge to get all customers is a price that is a little bit lower than the one of firm \(B\), that is, 49.99 million US Dollars. Now Airbus obtains the entire demand and makes a profit of \(\pi_{A}=39.99D(p_{A})\). This profit is higher than the shared profit at equal prices if firm \(A\) charges a price only slightly below the price of firm \(B\).

But of course, if Airbus charges a price slightly below the price of Boeing, then Boeing has no demand and makes a profit of zero. By charging a slightly lower price than Airbus it can obtain the entire demand and make a positive profit. Put differently, each firm wants to undercut the price of the rival to obtain the entire market demand. The incentive to undercut the rival only disappears when charging a lower price does not increase profits, which happens at a price equal to marginal costs.

If the competitor prices at a level equal to marginal costs it does not make sense for the other firm to charge a higher or lower price. (At a higher price, the firm has no customers; at a price below marginal costs the firm makes a loss). In Bertrand competition, this result is independent of the number of firms, which means that even if there are only two firms in the market prices are equal to marginal costs and profits are zero (as in perfect competition).

Suggested Opportunities

• Master's Program
• Posted 2 days ago

Master Data and Economics for Public Policy - Ecole polytechnique/ENSAE Paris/Télécom Paris

Starts 1 Sep at Ecole Polytechnique in Palaiseau, France

Jun 30, 2027 814900 80 Ecole Polytechnique

• Master's Program
• Posted 1 day ago

Individually tailored Master in Economics

Starts 1 Oct at Leuphana University of Lüneburg in Lüneburg, Germany

80 80 Leuphana University of Lüneburg

• Master's Program
• Posted 2 days ago

Master in Economics and Finance

Starts 1 Sep at CEMFI in Madrid, Spain

Jun 30, 2027 80 80 CEMFI

Let’s have a look at the best response functions of symmetric firms in a Bertrand game as shown in the figure below. The blue line is the best response function of firm 2 for a given price \(p_{1}\) and the green line is the best response function of firm \(1\); \(p_{M}\) denotes the monopoly price.

If you look closely you see that the green line is slightly below the 45-degree line (at points on the 45-degree line both firms charge the same price) if the price of firm 2 is above marginal costs and below the monopoly price. For any price charged by firm 2 in this interval, firm 1 will charge a price slightly below. The same is true for firm 2, of course. The best response functions are upward sloping because when a competitor has a higher price, it's optimal for the other firm to charge a price higher than their current price, but just below the competitor’s new high price.

The intersection of the two lines (the red dot) represents the unique Nash equilibrium of the game. There is only one point at which firms are playing a mutual best response and no firm has an incentive to deviate given the price chosen by the competitor. As we can see in the figure, this is the point at which the price is equal to marginal costs.

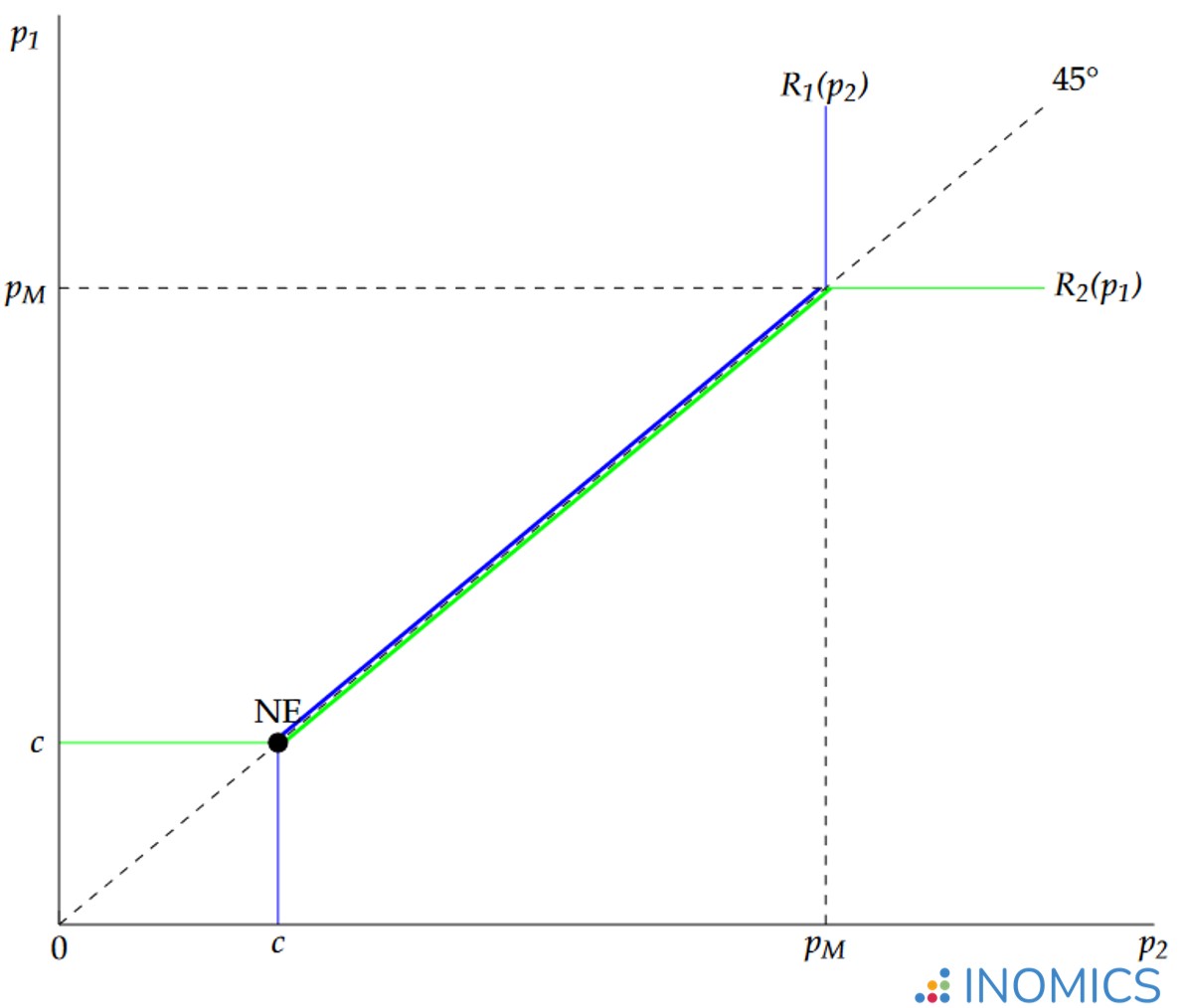
Figure 1: best response functions

Further reading

In Bertrand competition, when firms are not equally efficient - meaning one firm has lower marginal costs of production than the other firms - then the firm with the lowest marginal cost will obtain the entire demand and make a positive profit. Spulber shows in “Bertrand competition when rivals’ costs are unknown” (The Journal of Industrial Economics, 1995) that both firms price above marginal costs and obtain positive profits if the firms do not know the cost function of the competitor.

Good to know

In real-world markets, firms usually make positive profits. Why is that? First of all, firms rarely offer perfectly homogeneous goods. Even though the physical good that two firms are selling may be the same, goods produced or sold by different firms are not perceived as being identical (perfect substitutes) by consumers.

Consumers may prefer to buy a good at a particular firm for a variety of reasons. For example, the firm's shop might have a more convenient location, consumers might be loyal to a specific brand, or perhaps different services are offered with the good.

Second, in the classical Bertrand game firms interact only once. In real world markets, however, the same firms interact repeatedly day after day and may cooperate to maintain prices above marginal costs. Third, firms may be capacity constrained which means that they might not be able to produce enough to serve the entire market. As a consequence, the firm charging the higher price will not lose all customers to the competitor because the competitor cannot produce enough to serve the entire market. So, a firm in this situation can make a positive profit even if it charges a price above marginal costs.