Elasticity of substitution measures the ease with which one can switch between factors of production. The concept has a broad range of applications. For example, it can be used to compare labour and capital in firms, or native versus immigrant workers in the labour market. Additionally, it can assess 'clean' versus 'dirty' methods of production for environmental economics.

In order to calculate an elasticity of substitution, it is first necessary to determine an isoquant. From there, one must work out input ratios and marginal rates of technical substitution (or MRTS) along the isoquant. An isoquant represents combinations of inputs \(x_{1}\) and \(x_{2}\), which are required to produce a given level of output \(\overline{Y}\). These combinations along the blue isoquant \(f\left(x_{1},x_{2}\right)=\overline{Y}\) are visible in the graph below.

For any given point \(\left(x_{1},x_{2}\right)\) on the isoquant \(f\left(x_{1},x_{2}\right)=\overline{Y}\), it is possible to compute the input ratio. This is simply the quantity of one input divided by the other \(\frac{x_{2}}{x_{1}}\), as depicted by the gradients of the pink and grey lines in the graph.

Any production technique that uses inputs \(x_{1}\) and \(x_{2}\) to achieve output \(\overline{Y}\) will have an input ratio specific to that particular technique. For any given point \(\left(x_{1},x_{2}\right)\) on the isoquant \(f\left(x_{1},x_{2}\right)=\overline{Y}\) one can also calculate the marginal rate of technical substitution \(\frac{-dx_{2}}{dx_{1}}\). This is the rate at which input \(x_{1}\) can be exchanged for input \(x_{2}\) while maintaining the level of output at \(\overline{Y}\).

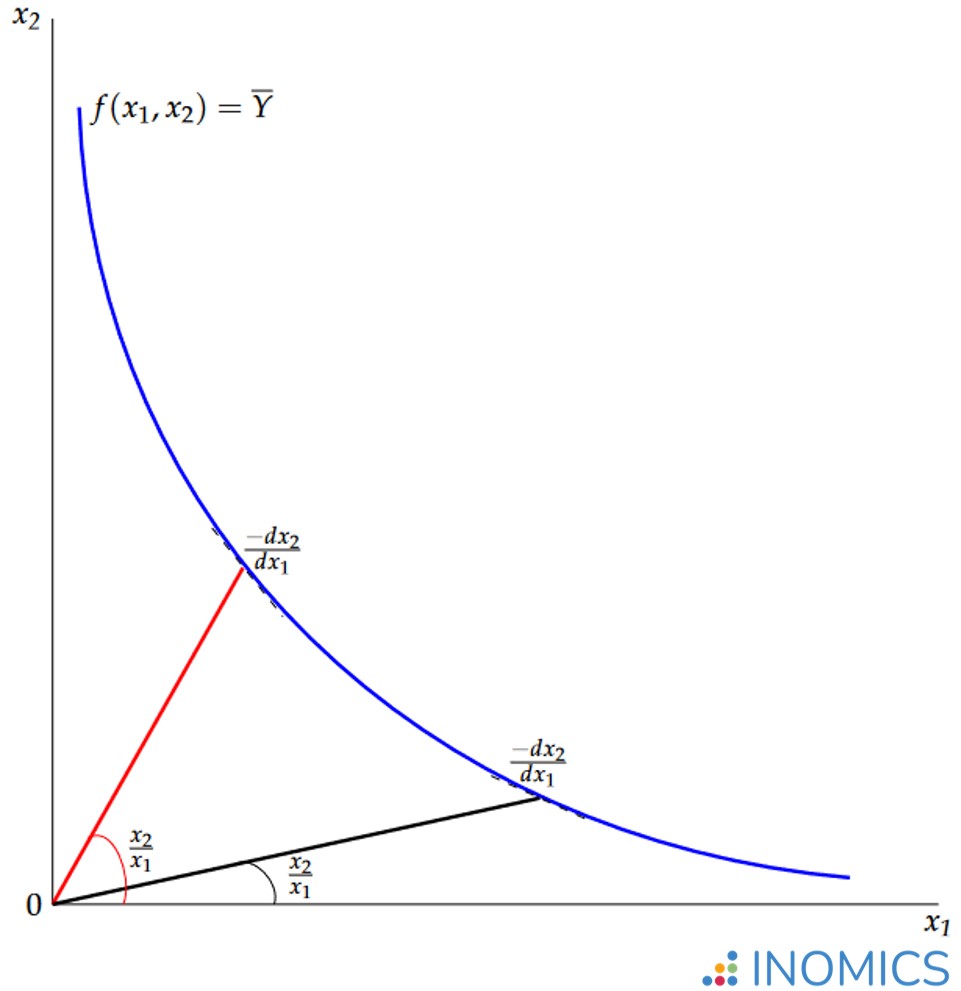
Figure 1: Elasticity of substitution along a curve

In essence, elasticity of substitution \(\sigma\) measures how easy it is to move between points along an isoquant. When moving between such points there are changes in both the input ratio and the marginal rate of technical substitution. 

Elasticity of substitution sets proportionate changes in the input ratio against proportionate changes in the marginal rate of technical substitution such that \[\sigma=\frac{\frac{\Delta\left(x_{2}/x_{1}\right)}{x_{2}/x_{1}}}{\frac{\Delta\left(-dx_{2}/dx_{1}\right)}{-dx_{2}/dx_{1}}}.\]

A positive value of \(\sigma\) indicates a certain degree of substitutability between production inputs. For the extreme case of perfect substitutes, elasticity of substitution approaches infinity \(\sigma\rightarrow\infty\). 

Electricity from two different suppliers could be seen as an example of a perfect substitute. Indeed, the electricity does the same job of powering production, regardless of the supplier.

On the other hand, a value of \(\sigma=0\) indicates just the opposite: the inputs cannot substitute for each other, as they are perfect complements. Therefore, one cannot be employed without also employing the other. For example, in car production, wheels require tires: neither is sufficient on its own. Thus wheels and tires are perfect complements.

In general, elasticity of substitution changes at different points along an isoquant. For example, it may be harder to swap machines for people (low \(\sigma\)) when only a few people are involved in production. On the contrary, it is easier to introduce machines (high \(\sigma\)) while there are still enough people to run the machines. 

However, a special case is one in which the elasticity of substitution is at a constant level for any combination of production inputs. That is, \(\sigma\) is the same value at any point along the isoquants that represent the production function. 

In practice, this is somewhat unrealistic but it simplifies the mathematics considerably, in particular for empirical modelling. This explains why the assumption of Constant Elasticity of Substitution (CES) is popular among economists studying production. The best-known example of a CES production function is the Cobb-Douglas production function.

The decision about how to organise production depends both on the substitutability of production inputs (value of \(\sigma\), shape of isoquants) and on the relative cost of the inputs to one another, which can be represented by means of isocost lines. 

For example, if an energy firm produces electricity both through an environmentally friendly source (e.g. wind) and by burning a carbon fuel then how much of each input (wind or carbon fuel) the firm allocates to electricity production will come down to their relative cost. 

Of course, if the firm suffers a bad reputation for causing harm to the environment then the reputational cost could also be internalised within the production cost. This would make it more likely for the firm to choose or increase its use of the green source. Alternatively, governments could seek to regulate the market for electricity (see the articles on positive and negative externalities).

Further reading

For an application of elasticity of substitution to the theory of environmental economics, see the paper by economists Daron Acemoglu, Philippe Aghion, Leonardo Bursztyn, and David Hemous, “The environment and directed technical change” (American Economic Review, 2012). The authors compare ‘clean’ and ‘dirty’ technologies within a model of sustainable growth, offering recommendations for different types of government intervention that depend on the substitutability of inputs.

Good to know

The concept of elasticity of substitution is also applicable to the theory of demand, for the analysis of indifference curves and the substitutability of goods and services in consumption. The concept dates to the early 1930s, when it was originally developed simultaneously and independently by economists John Hicks and Joan Robinson. 

Ironically, one might argue that Hicks and Robinson were good substitutes for one another in the production of economic knowledge, with a mutually high value of \(\sigma\)! Nevertheless, from the student’s perspective, a good understanding of this concept requires some effort. As Thomas Edison once said, there is no substitute for hard work.