La concurrence Stackelberg décrit un modèle de marché oligopolistique basé sur un jeu stratégique non coopératif dans lequel une entreprise (le "leader") agit en premier et décide de la quantité à produire, tandis que toutes les autres entreprises (les "suiveurs") décident ensuite de la quantité à produire. Cette structure séquentielle est la principale différence avec le modèle de Cournot, où les entreprises décident simultanément des quantités qu'elles produisent.

The leader might emerge in a market because of its size, reputation, innovative capacity, or because it simply started operating first. The leader will generally be better known and more recognized by customers, and is therefore better placed to decide first which quantity to sell. The follower(s) then decide(s) on their output after observing the leader's production choice.

Le modèle de leadership de Stackelberg a été développé en 1934 par l'économiste allemand Heinrich Freiherr von Stackelberg dans son livre "Market Structure and Equilibrium" (Structure de marché et équilibre).

 Les hypothèses du modèle de Stackelberg sont essentiellement les mêmes que celles du modèle de Cournot, à l'exception importante que les entreprises prennent leurs décisions en matière de quantité de production de manière séquentielle. Ces hypothèses sont les suivantes :

• Le marché compte un nombre fixe d'entreprises et celles-ci disposent d'un pouvoir de marché. Cela signifie que la décision de production de chaque entreprise affecte le prix du marché.
• Toutes les entreprises produisent un bien homogène et sont soumises aux mêmes fonctions de demande et de coût. En d'autres termes, il n'y a pas de différenciation des produits. Cela signifie que les biens produits par une entreprise sont totalement identiques aux yeux des consommateurs (ce sont des substituts parfaits).
• Les entreprises se concurrencent en termes de quantités produites. En d'autres termes, elles se disputent les parts de marché. C'est la principale différence avec la concurrence de Bertrand, dans laquelle les entreprises se font concurrence par les prix.
• Les entreprises décident séquentiellement de leur production, ce qui signifie que nous avons un modèle composé de deux périodes distinctes. Au cours de la première période, le leader choisit sa quantité de production. Cette décision ne peut plus être modifiée par la suite. Au cours de la seconde période, les entreprises suiveuses choisissent leur production après avoir observé la quantité choisie par le leader. C'est la principale différence par rapport à la concurrence de Cournot, dans laquelle les décisions de production de toutes les entreprises sont prises simultanément.
• Chaque entreprise agit stratégiquement en supposant que son ou ses concurrents ne modifieront pas leur production et décide de sa propre quantité de production de manière à maximiser son profit compte tenu de la production de ses concurrents.
• Les entreprises ne coopèrent pas.

L'équilibre Stackelberg-Nash

Pour dériver l'équilibre de Stackelberg-Nash, nous nous concentrerons sur l'exemple d'un duopole. C'est-à-dire qu'il n'y a que deux entreprises sur le marché. Nous supposerons que l'entreprise 1 (leader) et l'entreprise 2 (suiveur) produisent toutes deux le même bien au même coût de production c₁ = c₂ = c.

Nous supposerons également que les deux entreprises sont confrontées à la même fonction de demande linéaire donnée par :

p(Q) = a - bQ

où a > 0 and b > 0.

La quantité totale du marché est la somme de la production du leader (q₁) et du suiveur (q₂), soit Q = q₁ + q₂. Nous pouvons substituer cette expression pour Q dans les équations suivantes. La recette totale de l'entreprise 1 est alors donnée par le prix du marché p(Q) multiplié par la quantité produite :

\begin{equation*}
    r_1=p(Q)q_1=(a-b(q_1+q_2))q_1 \quad \text{(analogue pour l'entreprise 2)},
\end{equation*}

et les bénéfices totaux de l'entreprise 1 sont calculés comme la différence entre les recettes et les coûts de production :

\begin{equation*}
    \pi_1= p(Q)q_1-cq_1=(a-b(q_1+q_2)-c)q_1 \quad \text{(analogue pour l'entreprise 2)}.
\end{equation*}

Nous supposerons ici que a > c, qui est une condition nécessaire pour que des profits positifs puissent être réalisés.

Chaque entreprise choisit la quantité de production qui maximise ses profits, en tenant compte de la quantité produite par les autres entreprises sur le marché. Pour trouver l'équilibre de Nash de ce jeu séquentiel, nous devons utiliser l'induction à rebours. En d'autres termes, nous résolvons d'abord le problème d'optimisation pour le suiveur au cours de la deuxième période et, grâce à cette information, nous déterminons le choix optimal du leader au cours de la première période.

Au cours de la deuxième période, l'entreprise 2 (suiveur) choisit q₂, en tenant compte de la quantité produite par le leader au cours de la première période. Ainsi, pour obtenir la production optimale, il faut trouver la quantité q₂ qui maximise la fonction de profit de l'entreprise 2, en prenant q₁ comme donnée. Pour l'entreprise 2, le problème est donc similaire au modèle de Cournot :

\begin{align*}
    \max_{q_2} \{\pi(q_2) &=(a-b(q_1+q_2)-c)q_2\} \\
    \frac{\partial \pi(q_2)}{\partial q_2} &= a-bq_1-2bq_2-c = 0  \quad  | \quad \text{résoudre pour q2} \\
    q_2^* &= R_2(q_1)= \frac{a-bq_1-c}{2b} \quad \text{= fonction de réaction de Cournot}.
\end{align*} 

Comme dans le modèle de Cournot, l'équation R₂(q₁) est la meilleure fonction de réaction de l'entreprise 2 à toute quantité produite par l'entreprise 1.

Au cours de la première période, l'entreprise 1 (leader) choisit q₁, étant entendu que l'entreprise 2 réagira à ce choix au cours de la deuxième période en fonction de sa fonction de réaction R₂(q₁). Pour calculer la quantité optimale produite par l'entreprise 1, nous insérons donc la réponse optimale de l'entreprise 2 dans la fonction de profit de l'entreprise 1 à la place de q₂, puis nous prenons la dérivée première :

\begin{align*}
    \max_{q_1} \{\pi(q_1) &=(a-b(q_1+R_2(q_1))-c)q_1=aq_1-bq_1^2-bq_1R_2(q_1)-cq_1\} \\
    & \quad  \text{remarque : utiliser la règle du produit pour différencier$-bq_1R_2(q_1)$} \\
    \frac{\partial \pi(q_1)}{\partial q_1} &= a-2bq_1-bR_2(q_1)-bq_1R_2'(q1)-c = 0  \quad  | \quad \text{insérer $R_2$ and $R_2'$} \\
    & \Leftrightarrow a-2bq_1-b\left[\frac{a-bq_1-c}{2b}\right]+bq_1\frac{1}{2}-c = 0  \quad  | \quad \text{résoudre q1} \\
    & \Leftrightarrow a-2bq_1-\frac{a}{2}+\frac{bq_1}{2}+\frac{c}{2}+\frac{bq_1}{2}-c=0 \\
    & \Leftrightarrow \left[\frac{a-c}{2}\right]-bq_1=0 \\
    & \Leftrightarrow q_1^*= \frac{a-c}{2b} > \frac{a-c}{3b} = q_{Cournot}^*.
\end{align*}

Étant donné la quantité produite par le leader, q₁^*, nous pouvons alors calculer la production produite par le suiveur :

\begin{align*}
    q_2^* &= \frac{a-bq_1^*-c}{2b} = \left[\frac{a-c}{2b}\right]-q_1^*\frac{1}{2} \quad  | \quad \text{insérer $q_1^*$} \\
    \Leftrightarrow q_2^* &= \left[\frac{a-c}{2b}\right]-\frac{1}{2}\left[\frac{a-c}{2b}\right] \\
    \Leftrightarrow q_2^* &= \frac{a-c}{4b} < \frac{a-c}{3b} = q_{Cournot}^*.
\end{align*} 

Ainsi, dans l'équilibre de Stackelberg-Nash, le leader produit une plus grande quantité et le suiveur une plus petite quantité que ce que les mêmes entreprises auraient produit dans l'équilibre de Cournot-Nash. La figure ci-dessous illustre la différence entre les quantités produites dans un oligopole de Stackelberg ou de Cournot (concurrence imparfaite) ou dans un marché monopolistique (l'entreprise 1 est la seule entreprise sur le marché), où q₁^S > q₁^C et q₂^S < q₂^C:

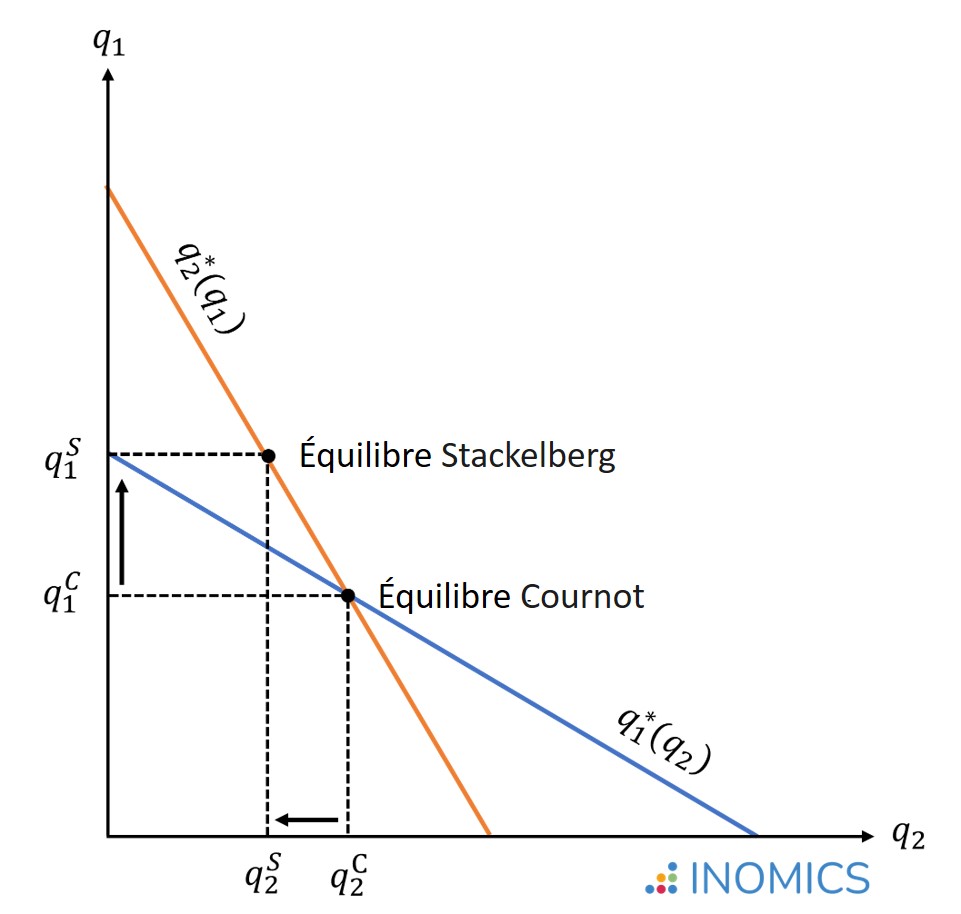
En calculant la quantité totale et le prix du marché, étant donné q₁^* et q₂^*, nous constatons que le jeu séquentiel de Stackelberg conduit à un équilibre plus concurrentiel - caractérisé par une production totale plus importante et un niveau de prix plus bas - que le jeu simultané de Cournot :

\begin{align*}    
    Q^* &=  q_1^* +  q_2^* = \frac{a-c}{2b} + \frac{a-c}{4b} = \frac{3}{4} \left[\frac{a-c}{b}\right] > \frac{2}{3} \left[\frac{a-c}{b}\right] = Q_{Cournot}^* \\
    p^* &= a - bQ^*= a - \frac{3}{4}(a-c) = \frac{a+3c}{4} < \frac{a+2c}{3} = p_{Cournot}^*.
\end{align*}

Le leader de Stackelberg tient compte du fait qu'une production plus élevée incite le suiveur à produire moins, mais aussi du fait qu'une production plus élevée fait baisser le niveau des prix. Dans ce scénario particulier, avec une fonction de demande linéaire et des coûts identiques, les deux effets s'annulent exactement et, dans ce cas, nous aboutissons à une solution où le leader de Stackelberg produit la quantité de monopole (bien qu'en raison de la baisse du niveau des prix, il reçoive des profits inférieurs à ceux du monopole).

Si nous insérions les quantités produites et le niveau des prix dans les fonctions de profit, nous constaterions que le leader de Stackelberg a des profits plus élevés, et le suiveur de Stackelberg des profits plus faibles, que les mêmes entreprises dans le modèle de Cournot. Le bénéfice supplémentaire dont bénéficie le leader par rapport au suiveur est dû au fait qu'il prend une décision de production en premier, ce qui signifie que le suiveur doit accepter la production du leader comme étant donnée et produire une production plus petite pour lui-même. C'est ce qu'on appelle l'avantage du premier arrivé.

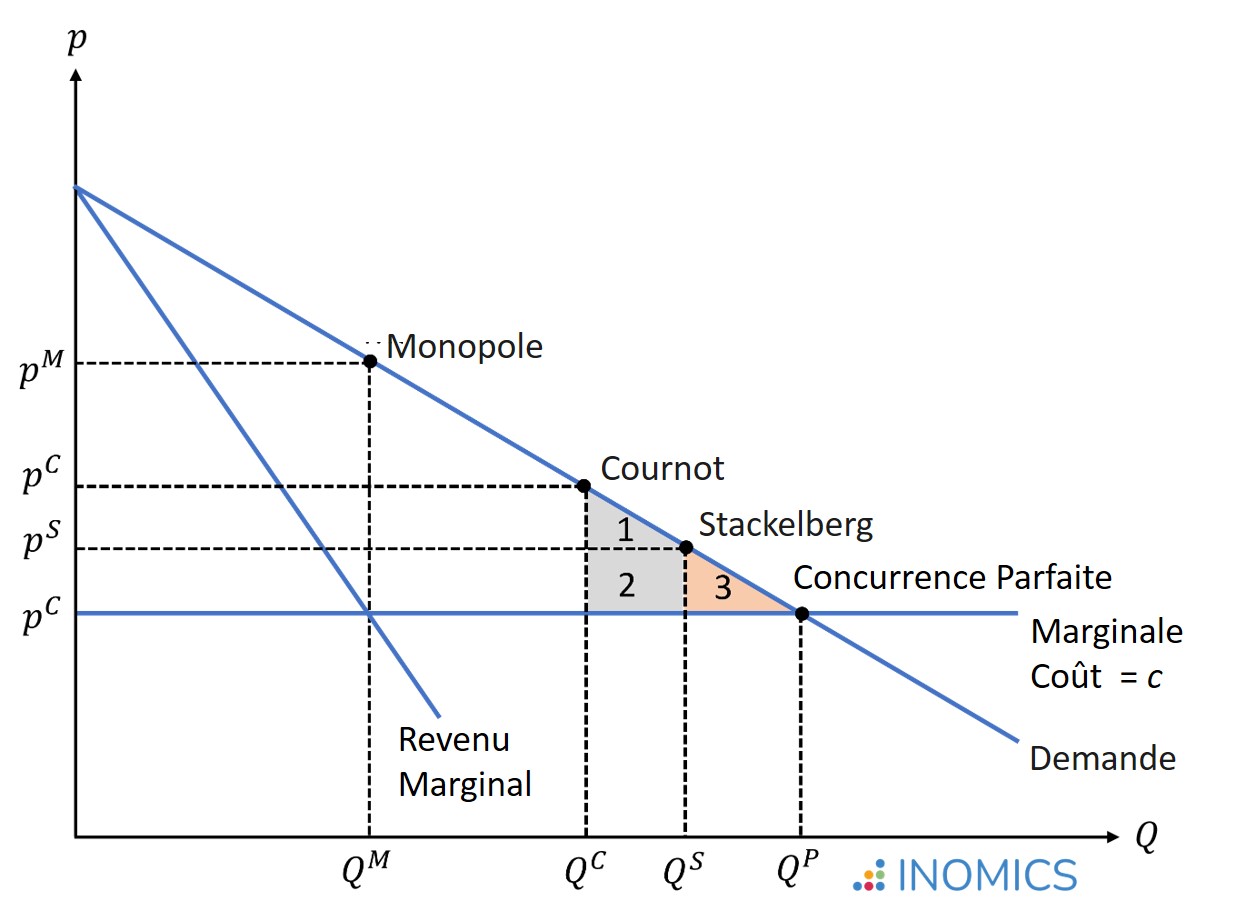
Dans la figure ci-dessous, les zones 1 + 2 illustrent le gain de bien-être dans le modèle de Stackelberg par rapport au modèle de Cournot, tandis que la zone 3 illustre la perte sèche restante par rapport à une situation de concurrence parfaite. Il est important de noter que l'équilibre de Stackelberg n'est plus efficace que l'équilibre de Cournot que si les entreprises sont symétriques, c'est-à-dire si les deux entreprises ont le même coût de production. Si le leader avait des coûts de production plus élevés et était donc moins efficace que le suiveur, l'équilibre de Cournot serait préférable du point de vue du bien-être, puisque le modèle séquentiel de Stackelberg donnerait un avantage à l'entreprise la moins efficace dont les coûts sont les plus élevés.

Bon à savoir

Les marchés réels peuvent présenter une concurrence de type Stackelberg lorsque, par exemple, des entrées séquentielles sur le marché ou des courses à la recherche et au développement placent une entreprise dans une meilleure position que ses concurrents. Prenons l'exemple de Microsoft dans les années 1990.

Considérons le marché des systèmes d'exploitation que nous utilisons pour interagir avec nos ordinateurs. Microsoft était le leader du marché des systèmes d'exploitation dans les années 1990, avec plus de 90 % de parts de marché grâce à son système d'exploitation Windows. Du fait de cette position sur le marché, les applications logicielles devaient généralement être compatibles avec le système d'exploitation de Microsoft. Les décisions de Microsoft en matière de production ont éclipsé toutes les entreprises suivantes, qui ont dû tenir compte de la part de marché massive de Microsoft (ou concevoir un plan pour s'approprier une partie de cette part de marché) lorsqu'elles ont pris des décisions en matière de production.

Les ordinateurs Apple ont fini par devenir populaires eux aussi, et le DOS d'Apple a pris quelques parts de marché aux systèmes d'exploitation Windows de Microsoft. Bien entendu, dans la vie réelle, les gens ont généralement une préférence marquée pour un Mac ou un PC. C'est là que l'exemple diffère du modèle de Stackelberg dont nous avons parlé dans cet article, car les systèmes d'exploitation ne sont pas identiques aux yeux des consommateurs. Bien que les produits soient similaires, dans la réalité, il y aura presque toujours une différenciation des produits et des prix qui fera que la dynamique du marché s'écartera du modèle stylisé.