La competencia de Stackelberg describe un modelo de mercado de oligopolio basado en un juego estratégico no cooperativo donde una empresa (el “líder”) se mueve en primer lugar  y decide cuánta cantidad producir, mientras que todas las demás empresas (los “seguidores”) deciden cuánto producir tras la decisión del líder. Esta estructura secuencial es la principal diferencia respecto al modelo de Cournot, donde las empresas deciden simultáneamente sobre las cantidades que producen.

El líder puede aparecer en un mercado a raíz de su tamaño, reputación, capacidad innovativa, o simplemente porque comenzó a operar en primer lugar. El líder es generalmente mejor conocido y más reconocido por sus clientes, y está por lo tanto mejor posicionado para tomar la primera decisión sobre la cantidad que vender. El o los seguidores deciden entonces sobre su producción, una vez observada la decisión de producción del líder.

El modelo de liderazgo de Stackelberg fue desarrollado en 1934 por el economista alemán Heinrich Freiherr von Stackelberg en su libro “Estructura de Mercado y Equilibrio” (Marktform und Gleichgewicht).

Las hipótesis del modelo de Stackelberg son en su mayoría iguales que en el modelo de Cournot, con la importante excepción de que las empresas toman sus decisiones sobre la cantidad de producción secuencialmente. Estas hipótesis son las siguientes:

• Existe un número fijo de empresas en el mercado y éstas tienen poder de mercado. Esto quiere decir que la decisión de producción de cada empresa afecta al precio de mercado.
• Todas las empresas producen un bien homogéneo, y están sujetas a las mismas funciones de demanda y del coste. En otras palabras, no hay diferenciación entre productos. Esto implica que los bienes producidos por cualquier empresa son completamente idénticos desde el punto de vista de los consumidores (son sustitutos perfectos).
• Las empresas compiten respecto a las cantidades que producen. Es decir, compiten por la cuota de mercado. Ésta es la principal diferencia en comparación con la competencia de Bertrand, donde las empresas compiten respecto a los precios.
• Las empresas deciden secuencialmente sobre la cantidad que producen, lo cual implica que tengamos un modelo basado en dos periodos distintos. En el primer periodo, el líder elige su cantidad de producción. Esta decisión no se podrá cambiar luego. En el segundo periodo, la(s) empresa(s) seguidora(s) elige(n) su producción tras observar la cantidad elegida por el líder. Ésta es la principal diferencia en comparación con la competencia de Cournot, donde las decisiones de producción son tomadas por todas las empresas simultáneamente.
• Cada empresa actúa estratégicamente sobre la hipótesis de que su(s) competidor(es) no cambiará(n) su producción, y decide su propia cantidad de producción con el objetivo de maximizar sus beneficios dada la producción de su(s) competidor(es).
• Las empresas no cooperan.

El Equilibrio de Nash en Stackelberg

Para derivar el equilibrio de Nash en Stackelberg, nos centraremos sobre el ejemplo de un duopolio. Es decir, tan solo hay dos empresas en el mercado. Asumiremos que tanto la empresa 1 (líder) como la empresa 2 (seguidor) producen el mismo bien bajo el mismo coste de producción c1 = c2 = c.

Adicionalmente asumiremos que ambas empresas hacen frente a la misma función de la demanda lineal descrita de la siguiente forma:

p(Q) = a - bQ

donde a > 0 y b > 0.

La cantidad total de mercado es la suma de la producción del líder (q₁) y del seguidor (q₂), es decir Q = q₁ + q₂. Podemos sustituir esta expresión para Q en las siguientes ecuaciones. El ingreso total de la empresa 1 es por lo tanto determinado por el precio de mercado p(Q) multiplicado por la cantidad producida:

\begin{equation*}
    r_1=p(Q)q_1=(a-b(q_1+q_2))q_1 \quad \text{(equivalente para la empresa 2)},
\end{equation*}

y los beneficios totales de la empresa 1 se calculan como la diferencia entre los ingresos y los costes de producción:

\begin{equation*}
    \pi_1= p(Q)q_1-cq_1=(a-b(q_1+q_2)-c)q_1 \quad \text{(equivalente para la empresa 2)}.
\end{equation*}

A partir de aquí asumiremos que a > c, siendo esto una condición necesaria para poder obtener beneficios positivos.

Cada empresa elige la cantidad de producción que maximice sus beneficios, teniendo en cuenta la cantidad producida por las demás empresas en el mercado. Para encontrar el equilibrio de Nash de este juego secuencial, necesitamos emplear la inducción hacia atrás. Es decir, primero resolvemos el problema de optimización para el seguidor en el segundo periodo, y con esta información determinamos la decisión óptima del líder en el primer periodo.

En el segundo periodo, la Empresa 2 (seguidor) elige q₂, teniendo en cuenta la cantidad producida por el líder en el primer periodo. Por lo tanto, para derivar la producción óptima, necesitamos encontrar la cantidad q₂ que maximice la función de los beneficios para la Empresa 2, tomando q₁ como dado. Para la Empresa 2, el problema es por lo tanto similar al del modelo de Cournot:

\begin{align*}
    \max_{q_2} \{\pi(q_2) &=(a-b(q_1+q_2)-c)q_2\} \\
    \frac{\partial \pi(q_2)}{\partial q_2} &= a-bq_1-2bq_2-c = 0  \quad  | \quad \text{solve for q2} \\
    q_2^* &= R_2(q_1)= \frac{a-bq_1-c}{2b} \quad \text{= función de reacción de Cournot}.
\end{align*}

Al igual que en el Modelo de Cournot, la ecuación R₂(q₁) es la función de mejor respuesta de la Empresa 2 ante cualquier cantidad producida por la Empresa 1.

En el 1^er periodo, la Empresa 1 (líder) elige q₁, con la consideración de que la Empresa 2 reaccionará a esta decisión en el segundo periodo de acuerdo con su función de reacción R₂(q₁). Para calcular la cantidad óptima producida por la Empresa 1, incluimos de esta manera la respuesta óptima de la Empresa 2 en la función de los beneficios de la Empresa 1 en el lugar de q₂ y luego tomamos la primera derivada:

\begin{align*}
    \max_{q_1} \{\pi(q_1) &=(a-b(q_1+R_2(q_1))-c)q_1=aq_1-bq_1^2-bq_1R_2(q_1)-cq_1\} \\
    & \quad  \text{Nota: Utilizar la regla del producto para diferenciar $-bq_1R_2(q_1)$} \\
    \frac{\partial \pi(q_1)}{\partial q_1} &= a-2bq_1-bR_2(q_1)-bq_1R_2'(q1)-c = 0  \quad  | \quad \text{insert $R_2$ and $R_2'$} \\
    & \Leftrightarrow a-2bq_1-b\left[\frac{a-bq_1-c}{2b}\right]+bq_1\frac{1}{2}-c = 0  \quad  | \quad \text{solve for q1} \\
    & \Leftrightarrow a-2bq_1-\frac{a}{2}+\frac{bq_1}{2}+\frac{c}{2}+\frac{bq_1}{2}-c=0 \\
    & \Leftrightarrow \left[\frac{a-c}{2}\right]-bq_1=0 \\
    & \Leftrightarrow q_1^*= \frac{a-c}{2b} > \frac{a-c}{3b} = q_{Cournot}^*.
\end{align*}

Dada la cantidad producida por el líder, q₁^*, podemos entonces calcular la cantidad producida por el seguidor:

\begin{align*}
    q_2^* &= \frac{a-bq_1^*-c}{2b} = \left[\frac{a-c}{2b}\right]-q_1^*\frac{1}{2} \quad  | \quad \text{insert $q_1^*$} \\
    \Leftrightarrow q_2^* &= \left[\frac{a-c}{2b}\right]-\frac{1}{2}\left[\frac{a-c}{2b}\right] \\
    \Leftrightarrow q_2^* &= \frac{a-c}{4b} < \frac{a-c}{3b} = q_{Cournot}^*.
\end{align*}

De esta manera, para el equilibrio de Nash en Stackelberg, el líder produce una mayor cantidad y el seguidor produce una cantidad inferior en comparación con lo que habrían producido estas mismas empresas en el equilibrio de Nash para Cournot. El gráfico inferior muestra la diferencia entre las cantidades producidas en un oligopolio de Stackelberg frente a uno de Cournot (competencia imperfecta) o mercado monopolístico (la empresa 1 es la única empresa en el mercado), donde q₁^S > q₁^C y q₂^S < q₂^C:

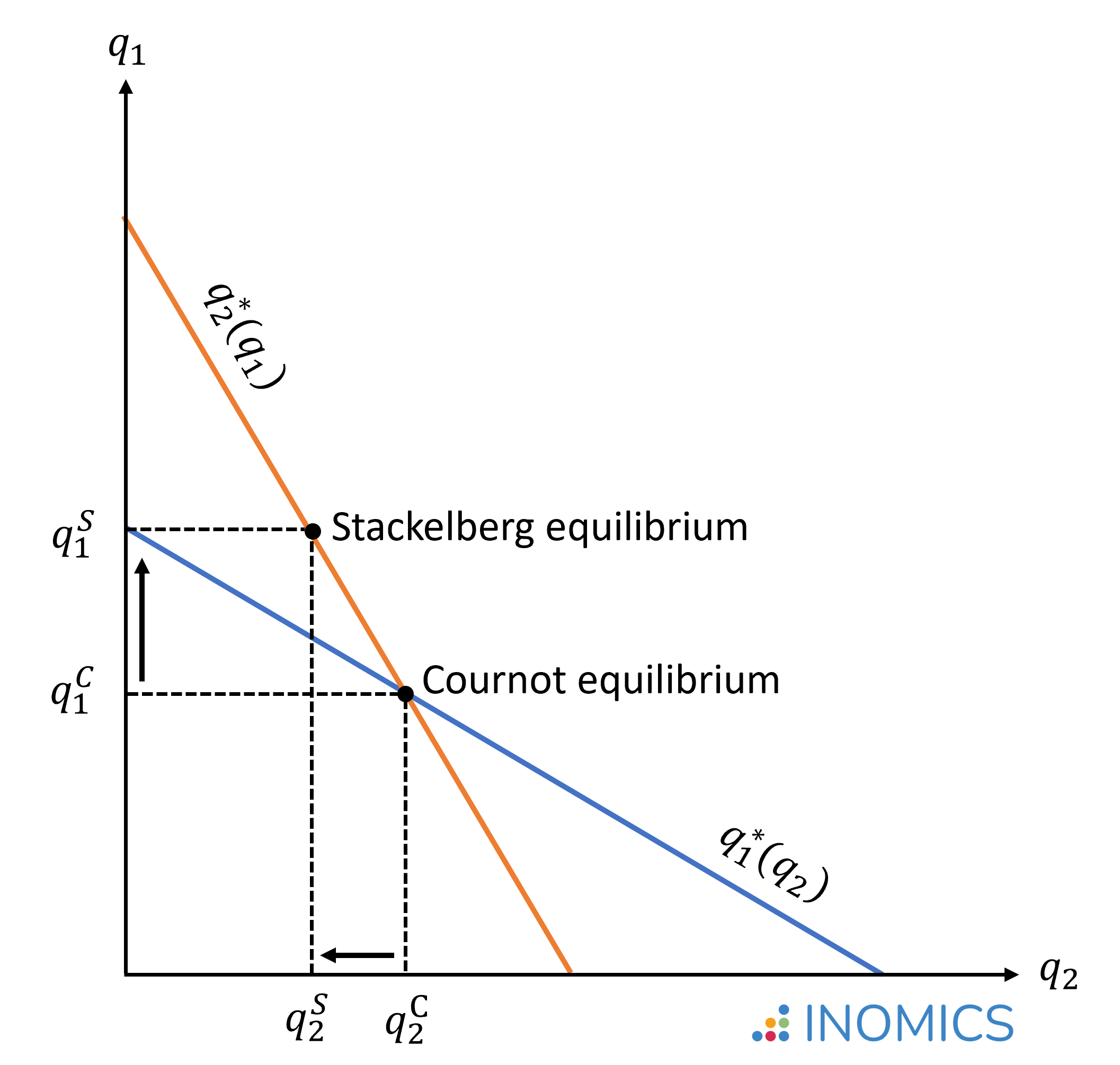
Calculando la cantidad total y el precio de mercado, dados q₁^* y q₂^*, podemos observar que el juego secuencial de Stackelberg da lugar a un equilibrio más competitivo – caracterizado por una mayor producción total y un nivel de precios inferior -- en comparación con el juego simultáneo de Cournot:

\begin{align*}    
    Q^* &=  q_1^* +  q_2^* = \frac{a-c}{2b} + \frac{a-c}{4b} = \frac{3}{4} \left[\frac{a-c}{b}\right] > \frac{2}{3} \left[\frac{a-c}{b}\right] = Q_{Cournot}^* \\
    p^* &= a - bQ^*= a - \frac{3}{4}(a-c) = \frac{a+3c}{4} < \frac{a+2c}{3} = p_{Cournot}^*.
\end{align*}

El líder en Stackelberg toma en consideración que una mayor producción conlleva que el seguidor produzca menos, pero también que una mayor producción da lugar a una presión sobre el nivel de precios. En este escenario en particular, con una función de la demanda lineal y costes idénticos, los dos efectos ocurren para cancelarse entre sí, por lo que en este caso terminamos con una solución donde el líder en Stackelberg produce la cantidad de un monopolio (si bien el nivel de precios es inferior, recibe menos beneficios que en el caso de un monopolio).

Si incluyésemos las cantidades de producción en las funciones de los beneficios, descubriríamos que el líder en Stackelberg tiene unos beneficios más altos, y el seguidor en Stackelberg tiene unos beneficios más bajos, en comparación con las mismas empresas en el modelo de Cournot. Este beneficio adicional que el líder obtiene en comparación con el seguidor, se debe a que el líder toma la decisión de producción primero, por lo que el seguidor debe aceptar la producción del líder como tal y asumir que su producción en particular será inferior. Ésta es la llamada ventaja de ser el primero.

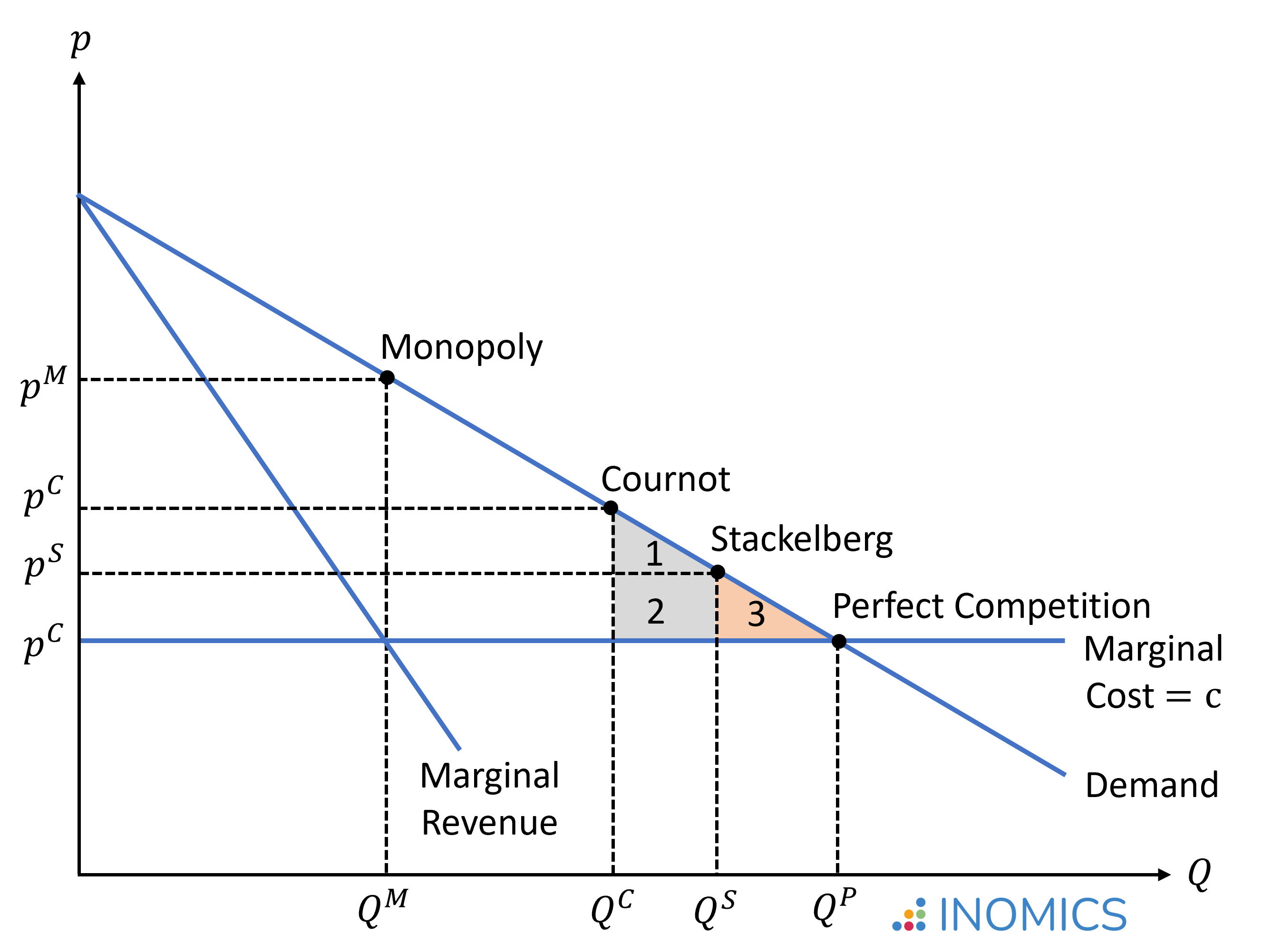
En el gráfico inferior, las áreas 1 + 2 muestran el bienestar ganado en el modelo de Stackelberg en comparación con el modelo de Cournot, mientras que el área 3 muestra la pérdida irrecuperable de eficiencia restante en comparación con una situación de competencia perfecta. Sin embargo, lo más importante es que el equilibrio de Stackelberg es tan solo más eficiente que el equilibrio de Cournot si las empresas son simétricas; es decir, si ambas empresas tienen el mismo coste de producción. Si el líder tuviese unos costes de producción más altos y fuese por lo tanto menos eficiente que el seguidor, entonces el equilibrio de Cournot sería preferible desde el punto de vista de la riqueza, dado que el modelo secuencial de Stackelberg aventajaría a la empresa menos eficiente con unos costes más altos.

Conviene saber

Los mercados actuales pueden exhibir una competencia similar a la de Stackelberg cuando, por ejemplo, la entrada secuencial en el mercado o las luchas por la I+D pongan a una empresa en una mejor posición en el mercado frente a sus competidores. Vamos a considerar como ejemplo de esto el caso de Microsoft en los años 90.

Consideremos el mercado de sistemas operativos que utilizamos para nuestros ordenadores. Microsoft era el líder en el mercado de sistemas operativos en los 90, llegando a controlar más del 90% de la cuota de mercado con su popular Windows OS. A raíz de esta posición en el mercado, las aplicaciones informáticas normalmente necesitaban ser compatibles con el sistema operativo de Microsoft. Las decisiones de producción de Microsoft ensombrecían a cualquier empresa que le siguiese, quienes tenían que contabilizar la enorme cuota de mercado que Microsoft tenía (o, diseñar un plan para capturar cierta parte de la cuota de mercado para ellas mismas) a la hora de tomar decisiones de producción.

Eventualmente, los ordenadores desarrollados por Apple también se popularizaron, y el Apple DOS le quitó cierta cuota de mercado a los sistemas operativos de Windows de Microsoft. Evidentemente, en la vida real las personas normalmente tienen una mayor preferencia entre usar un Mac o un PC. Es aquí donde el ejemplo difiere del modelo de Stackelberg del que hemos hablado hasta ahora, dado que los sistemas operativos no son idénticos desde la perspectiva de los consumidores. Aunque los productos sean similares, en la realidad casi siempre habrá alguna diferenciación entre los productos y los precios, provocando que la dinámica del mercado se desvíe del modelo estilizado.