Der Cournot-Wettbewerb beschreibt ein Oligopol-Marktmodell, bei dem zwei oder mehr Unternehmen dasselbe Gut produzieren und um Marktanteile konkurrieren. Die konkurrierenden Unternehmen entscheiden gleichzeitig und unabhängig voneinander über die Produktionsmenge, die sie herstellen werden. Die von allen Unternehmen angebotene Gesamtmenge bestimmt dann den Marktpreis. Dies unterscheidet sich vom Bertrand-Wettbewerb, bei dem die Unternehmen über die Preise konkurrieren, oder vom Stackelberg-Wettbewerb, bei dem die Unternehmen ihre Produktionsmengen nacheinander auswählen.

Der französische Universalgelehrte Antoine Augustin Cournot (1801-1877), nach dem dieses Wirtschaftsmodell benannt ist, veranschaulichte diese Marktsituation am Beispiel von zwei Unternehmen, die Mineralwasserquellen ausbeuten und jeweils unbegrenzte Mengen zum Nulltarif produzieren können.

Nach dem Gesetz der Nachfrage besteht zwischen Menge und Preis ein umgekehrtes Verhältnis, d. h. eine negative Korrelation. Das heißt, ein höheres Produktionsniveau führt zu relativ niedrigeren Preisen und vice versa. Um den Gewinn zu maximieren, muss jedes Unternehmen diesen Kompromiss zwischen Menge und Preis unter Berücksichtigung des erwarteten Marktangebots seiner Konkurrenten berücksichtigen.

Dies stellt eine spielstrategische Situation dar (siehe auch Spieltheorie). Im Cournot-Nash-Gleichgewicht wählt jedes Unternehmen die Menge, die die "beste Antwort" auf die Produktionsmenge des Wettbewerbers darstellt.

Im Folgenden werden wir die Cournot-Gleichgewichtsmengen ableiten und den Marktpreis berechnen. Wir werden sehen, dass der Cournot-Wettbewerb zu einem effizienteren Marktergebnis führt, als wenn es nur ein Unternehmen auf dem Markt gäbe (Monopol). Im Vergleich zum Gleichgewicht bei vollkommenem Wettbewerb gibt es jedoch immer noch einen Effizienzverlust.

Modell-Annahmen

Werfen wir einen kurzen Blick auf die wichtigsten Annahmen des Cournot-Modells:

• Es gibt eine feste Anzahl von Unternehmen auf dem Markt und die Unternehmen haben Marktmacht. Dies bedeutet, dass die Produktionsentscheidungen jedes Unternehmens den Marktpreis beeinflussen.
• Alle Unternehmen produzieren ein homogenes Gut. Mit anderen Worten: Es gibt keine Produktdifferenzierung. Das bedeutet, dass die von jedem Unternehmen produzierten Güter in den Augen der Verbraucher völlig identisch sind (sie sind perfekte Substitute).
• Die Unternehmen konkurrieren in Bezug auf die von ihnen produzierten Mengen. Das heißt, sie konkurrieren um Marktanteile. Dies ist der entscheidende Unterschied zum Bertrand-Wettbewerb, bei dem die Unternehmen über die Preise konkurrieren.
• Jedes Unternehmen handelt strategisch in der Annahme, dass sein(e) Konkurrent(en) die Gleichgewichtsmenge wählen, und legt seine eigene Produktionsmenge so fest, dass es seinen Gewinn maximiert.
• Die Produktionsentscheidungen werden von allen Unternehmen gleichzeitig getroffen. Dies ist der Hauptunterschied zum Stackelberg-Wettbewerb, bei dem das führende Unternehmen zuerst handelt und die nachfolgenden Unternehmen nacheinander handeln.
• Die Unternehmen kooperieren nicht.

Das Cournot-Nash-Gleichgewicht

Um das Cournot-Nash-Gleichgewicht herzuleiten, werden wir uns auf das Beispiel eines Duopols konzentrieren. Das heißt, es gibt nur zwei Unternehmen auf dem Markt. Wir nehmen an, dass die Unternehmen 1 und 2 das gleiche Gut zu den gleichen Produktionskosten c₁ = c₂ = c herstellen.

Wir nehmen an, dass die Nachfrage eine lineare Funktion ist, die durch p(Q) = a - bQ gegeben ist, wobei a > 0 und b > 0 sind. Wenn ein Unternehmen q₁ und das andere q₂ produziert, dann ist die gesamte Marktmenge Q = q₁ + q₂. Wir können also diesen Ausdruck für Q in den folgenden Gleichungen ersetzen. Der Gesamtertrag von Unternehmen 1 ergibt sich dann aus dem Marktpreis mal der produzierten Menge:

\begin{equation*}
    r_1=pq_1=(a-b(q_1+q_2))q_1 \quad \text{(analogous for firm 2)},
\end{equation*}

und der Gesamtgewinn von Unternehmen 1 wird als Differenz zwischen den Einnahmen und den Produktionskosten berechnet:

\begin{equation*}
    \pi_1= pq_1-cq_1=(a-c-b(q_1+q_2))q_1 \quad \text{(analogous for firm 2)}.
\end{equation*}

Ab hier nehmen wir an, dass a > c ist, was eine notwendige Bedingung dafür ist, dass positive Gewinne erzielt werden können.

Jedes Unternehmen wählt dann die Produktionsmenge, die seine Gewinne maximiert, wobei die von seinem Konkurrenten produzierte Menge berücksichtigt wird. Um den optimalen Output zu ermitteln, müssen wir also die Menge q₁ finden, die die Gewinnfunktion für Unternehmen 1 maximiert, wobei q₂ als gegeben angenommen wird. Das Gleiche gilt für das Unternehmen 2. Um das Optimum zu finden, nehmen wir die partielle Ableitung der Gewinnfunktion und setzen diese Gleichung gleich 0:

\begin{align*}
    \max_{q_1} \{\pi(q_1) &=(a-c-b(q_1+q_2))q_1\} \\
    \frac{\partial \pi(q_1)}{\partial q_1} &= a-c-2bq_1-bq_2 = 0  \quad  | \quad \text{solve for q1} \\
    q_1^* &= \frac{a-c-bq_2}{2b} \\ \text{and analogously} \quad q_2^* &= \frac{a-c-bq_1}{2b}.
\end{align*}

Die Gleichungen q₁*(q₂) und q₂*(q₁) werden als Best-Response-Funktionen bezeichnet. Sie geben den optimalen Output von Unternehmen 1 für jede von Unternehmen 2 produzierte Menge an, und den optimalen Output von Unternehmen 2 für jede von Unternehmen 1 produzierte Menge.

Im Cournot-Nash-Gleichgewicht geben beide Unternehmen ihre beste Antwort auf die Aktionen des jeweils anderen. Zur Ableitung des Gleichgewichts setzen wir also die optimale Reaktion von Unternehmen 2 in die Gleichung von Unternehmen 1 ein, um dessen optimale Menge zu berechnen, und umgekehrt:

\begin{align*}    
    q_1 &= \frac{a-c-b\frac{a-c-bq_1}{2b}}{2b}  \quad  | \quad \text{solve for q1} \\
    q_1^* &= \frac{a-c}{3b} \\
    \text{and analogously} \quad q_2^* &= \frac{a-c}{3b} = q_1^*.
\end{align*}

Dies ist das einzige Nash-Gleichgewicht des Cournot-Duopols. Setzt man die optimalen Mengen in die Nachfragefunktion ein, erhält man die Gesamtmenge und den Marktpreis im Gleichgewicht:

\begin{align*}    
    Q^* &=  q_1^* +  q_2^* = \frac{2}{3} \left[\frac{a-c}{b}\right] \\
    p^* &= a - bQ^*= a - \frac{2}{3}(a-c) = \frac{a+2c}{3}.
\end{align*}

Grafisch gesehen liegt der Gleichgewichtspunkt E dort, wo sich die Best-Response-Kurven q₁*(q₂) und q₂*(q₁) schneiden. Die Abbildung zeigt auch die Mengen q₁^M und q₂^M, die produziert worden wären, wenn entweder Unternehmen 1 oder Unternehmen 2 das einzige auf dem Markt tätige Unternehmen gewesen wäre, d. h. wenn eines der beiden Unternehmen volle Monopolmacht hätte.

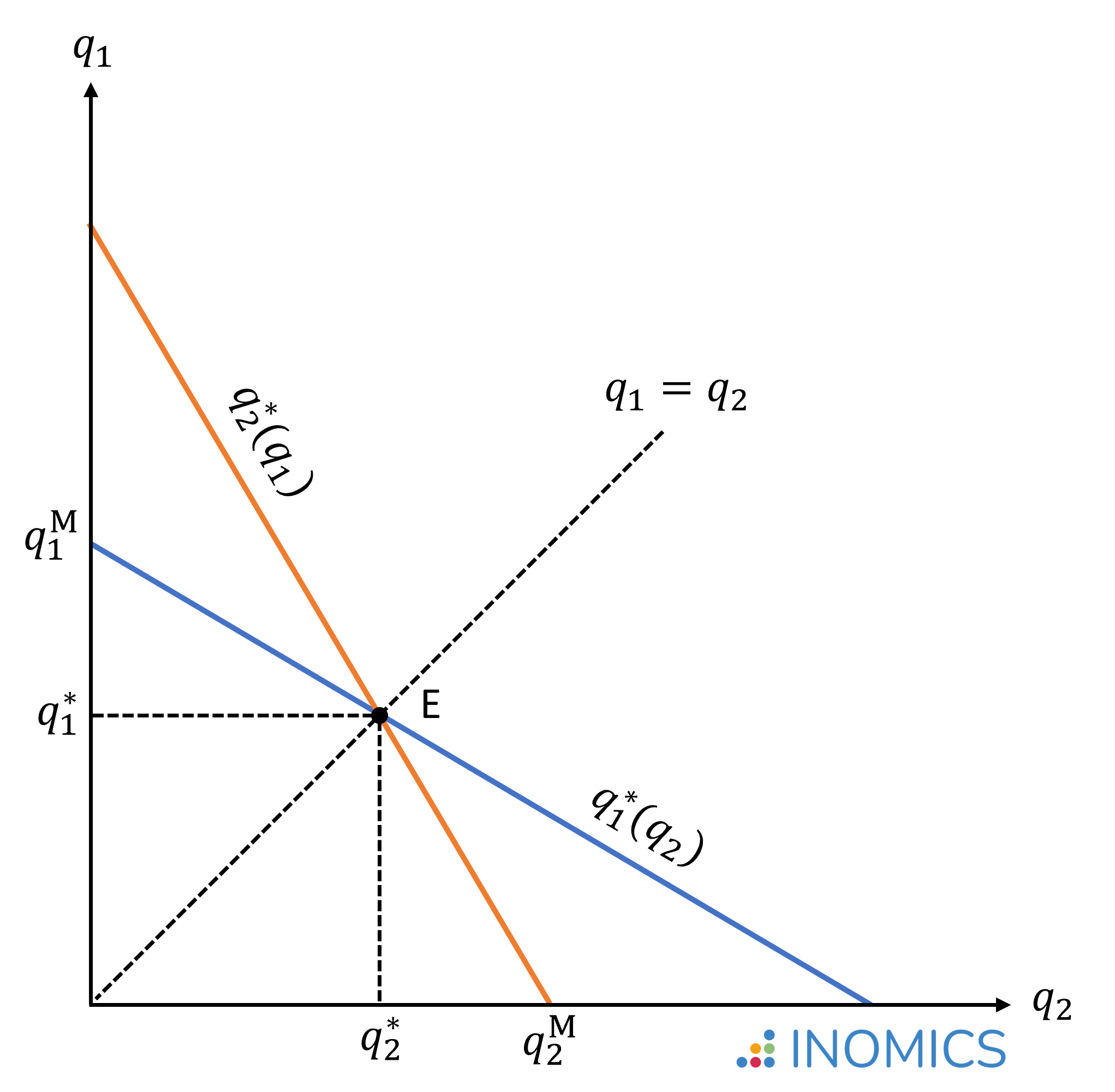
Abbildung 1: Cournot-Nash-Gleichgewicht

Wir können die oben abgeleitete Modelllösung auch verwenden, um die Monopol- und Cournot-Duopol-Situation zu vergleichen. Wenn wir annehmen, dass Unternehmen 1 der einzige Produzent ist, impliziert dies q₂ = 0 und somit:

\begin{align*}    
    q_1 &= \frac{a-c-bq_2}{2b}   \quad  | \quad q_2=0 \\
    \Longrightarrow q_1^M &= \frac{a-c}{2b}=Q^M \\
    \text{and}  \quad p^M &= a - bQ^M= a - \frac{1}{2}(a-c) = \frac{a+c}{2}.
\end{align*}

Daraus lässt sich schließen, dass im duopolistischen Cournot-Nash-Gleichgewicht die Gesamtmenge der Produktion größer und der Preis kleiner ist als im monopolistischen Marktgleichgewicht:

\begin{align*}    
    Q^* &= \frac{2}{3} \left[\frac{a-c}{b}\right] > \frac{1}{2} \left[\frac{a-c}{b}\right]=Q^M \\
    \text{and} \quad p^* &= \frac{a+2c}{3} < \frac{a+c}{2} = p^M \quad \text{if} \quad a>c.
\end{align*}

Dennoch bleibt ein Wohlfahrtsverlust im Vergleich zum Marktgleichgewicht bei vollkommenem Wettbewerb bestehen. Auf einem Markt mit vollkommenem Wettbewerb ist der Preis gleich den Grenzkosten und die Unternehmen erzielen keine Gewinne, d. h.pC = a - bQC = c. Daraus lässt sich schließen, dass im duopolistischen Cournot-Nash-Gleichgewicht die Gesamtmenge der produzierten Güter niedriger und der Preis höher ist als im Wettbewerbs Marktgleichgewicht:

\begin{align*}    
    Q^* &= \frac{2}{3} \left[\frac{a-c}{b}\right] < \frac{a-c}{b}=Q^C \\
    \text{and} \quad p^* &= \frac{a+2c}{3} > c = p^C \quad \text{if} \quad a>c.
\end{align*}

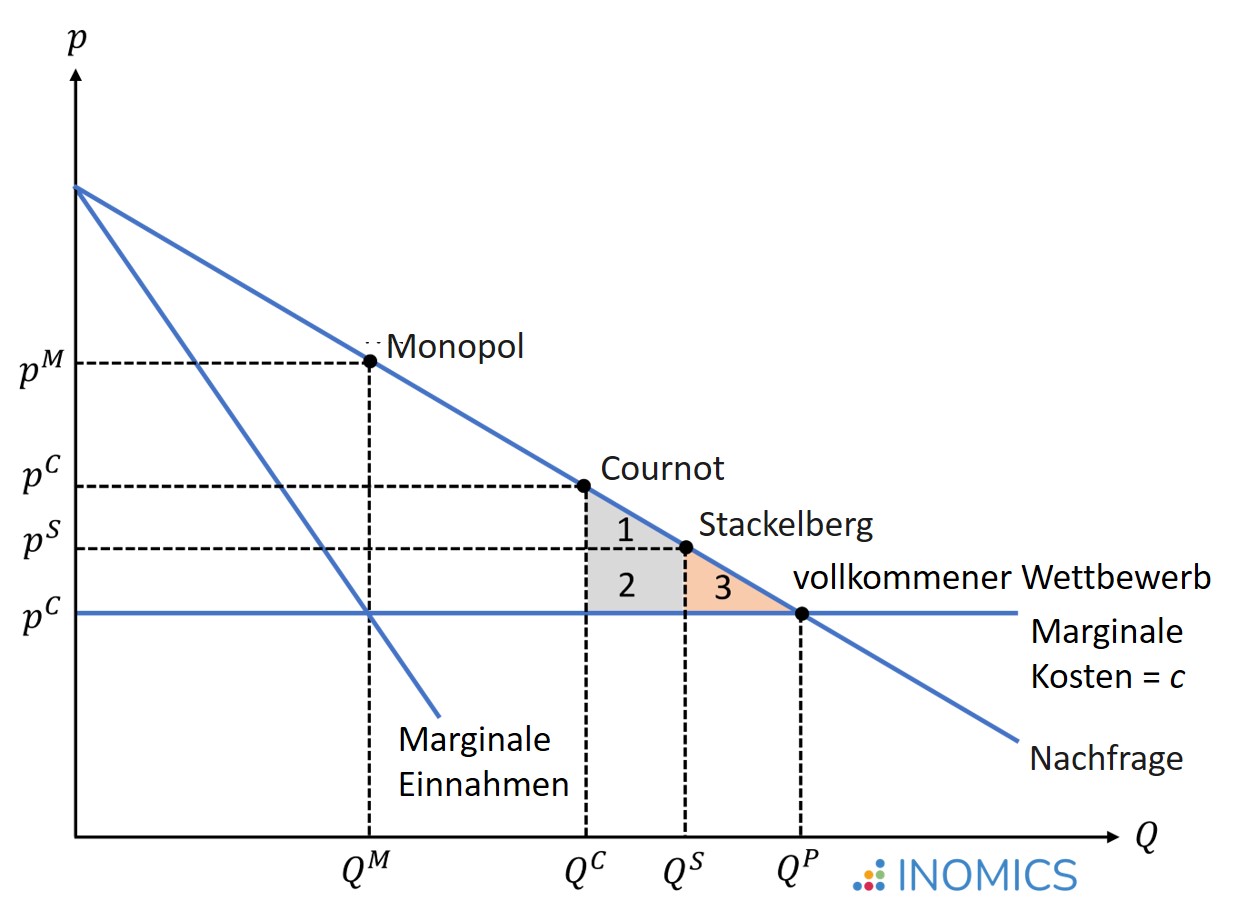
In der nachstehenden Abbildung, in der davon ausgegangen wird, dass die Grenzkosten über alle Produktionsbereiche hinweg konstant sind, werden die Markt Mengen und Preise dargestellt, die sich bei einem Monopol, einem Cournot-Oligopol und bei vollkommener Konkurrenz ergeben. Das Cournot-Nash-Gleichgewicht wird an einem Punkt zwischen der Monopol- und der vollkommenen Wettbewerbslösung auftreten.

Die Bereiche 1 und 2 veranschaulichen den Wohlfahrtsgewinn bei Cournot-Wettbewerb im Vergleich zu einem monopolistischen Markt, während Bereich 3 den verbleibenden Mitnahmeeffekt im Vergleich zu vollkommenem Wettbewerb veranschaulicht. Antoine Cournot argumentierte, dass sich die beiden Unternehmen auf dem Markt durch Absprachen und die Bildung eines Kartells der Monopollösung annähern könnten. Dies ist jedoch kein stabiles Nash-Gleichgewicht, da es für beide Unternehmen vorteilhaft wäre, davon abzuweichen (wie die Ableitung der Best-Response-Funktionen oben gezeigt hat).

Der Mitnahmeeffekt nimmt ab, wenn die Zahl der konkurrierenden Unternehmen auf dem Markt steigt. Wenn die Zahl der Unternehmen im Cournot-Oligopol gegen unendlich konvergiert, konvergiert das Cournot-Nash-Gleichgewicht gegen das Marktgleichgewicht bei vollkommener Konkurrenz.

Gut zu wissen

Die Organisation der erdölexportierenden Länder (OPEC) wird oft als gutes Beispiel für ein Cournot-Oligopol genannt. Untersuchungen haben gezeigt, dass das Verhalten der OPEC-Mitgliedsländer irgendwo zwischen einem nicht-kooperativen Cournot-Oligopol und einem Kartell liegt. Das heißt, dass es zwar eine gewisse Zusammenarbeit gibt, es aber insbesondere für kleinere OPEC-Produzenten (deren Produktion weniger Einfluss auf die Marktpreise haben kann) optimal sein kann, eine expansivere Produktionspolitik zu verfolgen. Die Studie von Okullo und Reynès (2016) bietet in dieser Hinsicht interessante Einblicke.