La competencia de Cournot describe un modelo de mercado de oligopolio donde dos o más empresas producen el mismo producto y compiten por su cuota de mercado. Las empresas competidoras deciden simultánea e independientemente de cada una sobre la cantidad del producto que generarán. La cantidad total ofertada por todas las empresas determina por tanto el precio de mercado. Esto difiere de la competencia de Bertrand, donde las empresas compiten respecto a los precios, o la competencia de Stackelberg, donde las empresas eligen secuencialmente las cantidades de producción.

El polímata francés, Antoine Augustin Cournot (1801–1877), a quien se debe el nombre de este modelo económico, ilustró esta situación de mercado utilizando como ejemplo dos empresas dedicadas a la explotación de manantiales de agua mineral, cada empresa con la capacidad de producir cantidades ilimitadas sin coste alguno.

De acuerdo con la ley de la demanda, existe una relación inversa, o correlación negativa, entre la cantidad y el precio. Es decir, cuanto mayor sea el nivel de producción los precios serán relativamente inferiores, y viceversa. Para maximizar los beneficios, cada empresa tiene que valorar este trade-off entre la cantidad y el precio, tomando en consideración la oferta de mercado de su competencia esperada.

Esto constituye una situación de juego estratégica (consulta también la teoría de juegos). En el equilibrio de Nash para Cournot, cada empresa elige la cantidad que representa la ‘mejor respuesta’ a la cantidad de producción de la competencia.  

Más en adelante derivamos las cantidades de equilibrio de Cournot y calculamos el precio de mercado. También veremos que la competencia de Cournot da lugar a un resultado de mercado más eficiente que en el caso en que hubiese tan solo una empresa en el mercado (monopolio). Sin embargo, aun así existe una pérdida de eficiencia en comparación con el equilibrio bajo la competencia perfecta.

Hipótesis del Modelo

A continuación, presentamos un rápido vistazo de las principales hipótesis del modelo de Cournot:

• Existe un número de empresas fijo en el mercado y estas empresas tienen poder de mercado. Esto quiere decir que la decisión de producción de cada empresa afecta al precio de mercado.
• Todas las empresas producen un bien homogéneo. En otras palabras, no existe diferenciación del producto. Esto quiere decir que los bienes producidos por cualquier empresa son completamente idénticos desde la perspectiva de los consumidores (son sustitutos perfectos).
• Las empresas compiten en relación con las cantidades que producen.  Es decir, compiten por la cuota de mercado. Esta es la diferencia clave con respecto a la competencia de Bertrand, donde las empresas compiten por los precios.
• Cada empresa actúa de forma estratégica sobre la suposición de que su(s) competidor(es) elegirá(n) la cantidad de equilibrio, y decide su propia cantidad de producción con el fin de maximizar sus beneficios.
• Las decisiones de producción de todas las empresas son tomadas de forma simultánea. Esta es la diferencia clave con respecto a la competencia de Stackelberg, donde la empresa líder toma el primer movimiento y, seguidamente las empresas seguidoras se mueven de forma secuencial.
• Las empresas no cooperan.

El equilibrio de Nash para Cournot

Para derivar el equilibrio de Nash para Cournot, nos fijaremos en el ejemplo de un duopolio, es decir, solamente hay dos empresas en el mercado. Asumiremos que las empresas 1 y 2 producen ambas el mismo bien bajo el mismo coste de producción c₁ = c₂ = c.

Asumimos que la demanda es una función lineal dada por p(Q) = a - bQ donde a > 0 y b > 0. Si una empresa produce q1 y la otra produce q₂, la cantidad total de mercado será entonces Q = q₁ + q₂. De esta manera, podemos sustituir esta expresión para Q en las siguientes ecuaciones. El ingreso total de la empresa 1 es por lo tanto determinado por el precio de mercado multiplicado por la cantidad producida:

\begin{equation*}
    r_1=pq_1=(a-b(q_1+q_2))q_1 \quad \text{(análogo para la empresa 2)},
\end{equation*}

y los beneficios totales de la empresa 1 se calculan como la diferencia entre el ingreso y los costes de producción:

\begin{equation*}
    \pi_1= pq_1-cq_1=(a-c-b(q_1+q_2))q_1 \quad \text{(análogo para la empresa 2)}.
\end{equation*}

A partir de aquí asumiremos que a > c, siendo esta condición necesaria para poder obtener beneficios positivos.

Cada empresa elige entonces la cantidad de producción que maximiza sus beneficios, tomando en consideración la cantidad producida por su competidor. Por lo tanto, para derivar la producción óptima, necesitamos fijar la cantidad q1 que maximice la función del beneficio para la empresa 1, tomando q2 como dado. De forma análoga, haremos lo mismo para la empresa 2. Para encontrar la cantidad óptima, tomaremos la derivada parcial de la función del beneficio e igualaremos la ecuación a 0:

\begin{align*}
    \max_{q_1} \{\pi(q_1) &=(a-c-b(q_1+q_2))q_1\} \\
    \frac{\partial \pi(q_1)}{\partial q_1} &= a-c-2bq_1-bq_2 = 0  \quad  | \quad \text{resuelve q1} \\
    q_1^* &= \frac{a-c-bq_2}{2b} \\ \text{y de forma análoga} \quad q_2^* &= \frac{a-c-bq_1}{2b}.
\end{align*}

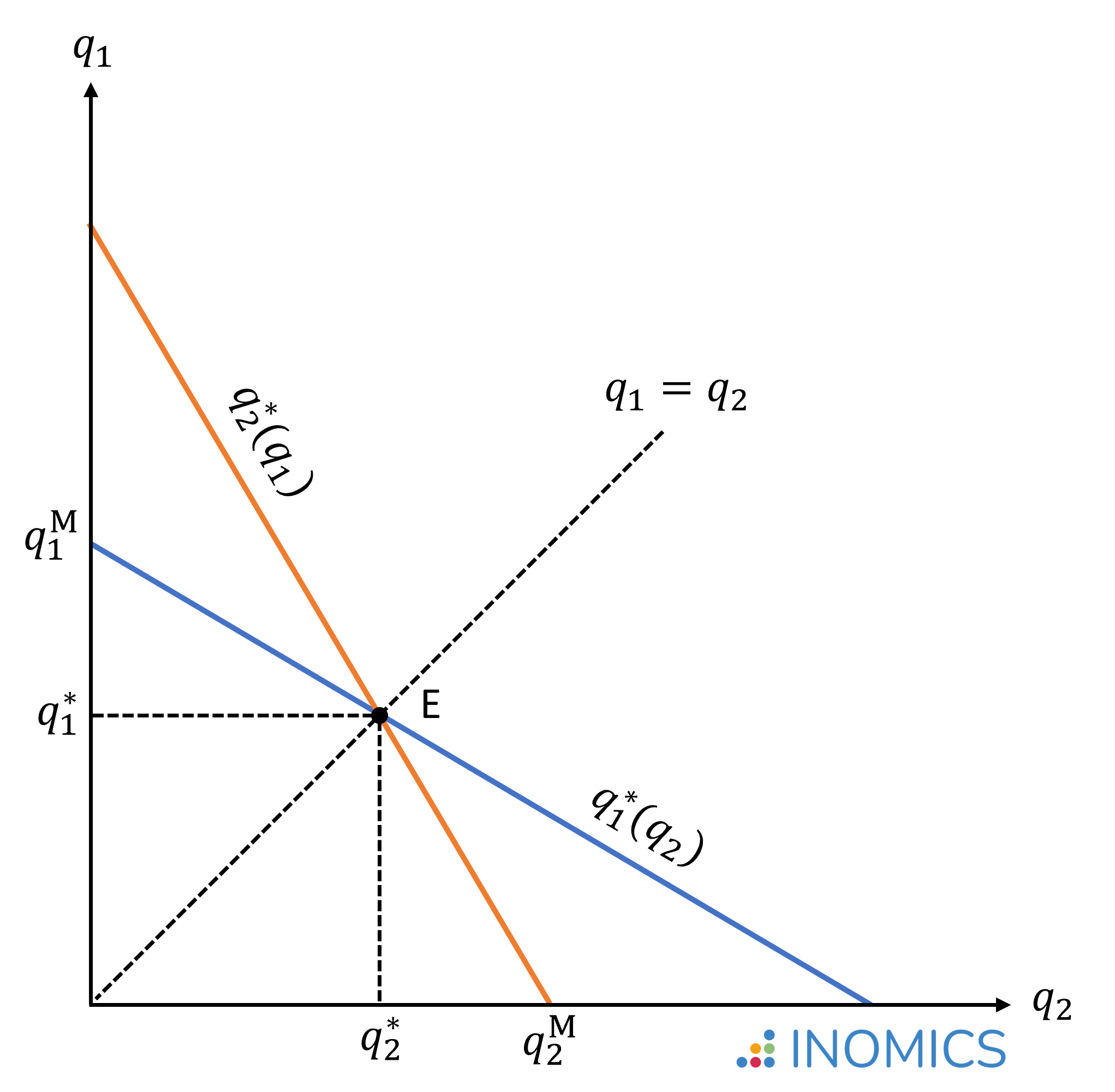
A las ecuaciones q₁*(q₂) y q₂*(q₁) se les llama funciones de mejor respuesta. Éstas nos dicen la producción óptima de la empresa 1 para cualquier cantidad producida por la empresa 2, y la producción óptima de la empresa 2 para cualquier cantidad producida por la empresa 1.

En el equilibrio de Nash para Cournot, ambas empresas darán su mejor respuesta respecto a las acciones de la otra. Para derivar el equilibrio, incorporaremos así la respuesta óptima de la empresa 2 en la ecuación de la empresa 1 para calcular su cantidad óptima, y viceversa:

\begin{align*}    
    q_1 &= \frac{a-c-b\frac{a-c-bq_1}{2b}}{2b}  \quad  | \quad \text{resuelve q1} \\
    q_1^* &= \frac{a-c}{3b} \\
    \text{y de forma análoga} \quad q_2^* &= \frac{a-c}{3b} = q_1^*.
\end{align*}

Éste es el único equilibrio de Nash para el duopolio de Cournot. Al incluir las cantidades óptimas dentro de la función de la demanda obtenemos la cantidad total y el precio de mercado en equilibrio:

\begin{align*}    
    Q^* &=  q_1^* +  q_2^* = \frac{2}{3} \left[\frac{a-c}{b}\right] \\
    p^* &= a - bQ^*= a - \frac{2}{3}(a-c) = \frac{a+2c}{3}.
\end{align*}

Gráficamente, el punto de equilibrio E se encuentra donde las curvas de mejor respuesta q₁*(q₂) y q₂*(q₁) se cruzan. El gráfico también ilustra las cantidades q₁^M y q₂^M que se habrían producido si la empresa 1 o la empresa 2 fuese la única operando en el mercado; es decir, si una de ambas empresas tuviese el poder de monopolio total.

También podemos utilizar la solución del modelo derivado arriba para comparar las situaciones de un monopolio frente a la del duopolio de Cournot. Si asumimos que la empresa 1 es el único productor, entonces q₂ = 0 y por lo tanto:

\begin{align*}    
    q_1 &= \frac{a-c-bq_2}{2b}   \quad  | \quad q_2=0 \\
    \Longrightarrow q_1^M &= \frac{a-c}{2b}=Q^M \\
    \text{y}  \quad p^M &= a - bQ^M= a - \frac{1}{2}(a-c) = \frac{a+c}{2}.
\end{align*}

A partir de esto podemos concluir que en el equilibrio duopolístico de Nash para Cournot, la cantidad total de producción es mayor y el precio es menor que en el equilibrio de un mercado monopolista:

\begin{align*}    
    Q^* &= \frac{2}{3} \left[\frac{a-c}{b}\right] > \frac{1}{2} \left[\frac{a-c}{b}\right]=Q^M \\
    \text{y} \quad p^* &= \frac{a+2c}{3} < \frac{a+c}{2} = p^M \quad \text{si} \quad a>c.
\end{align*}

Sin embargo, sigue existiendo una pérdida de bienestar en comparación con el equilibrio de mercado bajo una competencia perfecta. En un mercado perfectamente competitivo, el precio es igual al coste marginal y las empresas obtienen cero beneficios, por lo que p^C = a - bQ^C = c. A partir de esto podemos concluir que en el equilibrio duopolístico de Nash para Cournot, la cantidad total de producción es menor y el precio mayor que en el equilibrio de un mercado competitivo:

\begin{align*}    
    Q^* &= \frac{2}{3} \left[\frac{a-c}{b}\right] < \frac{a-c}{b}=Q^C \\
    \text{y} \quad p^* &= \frac{a+2c}{3} > c = p^C \quad \text{si} \quad a>c.
\end{align*}

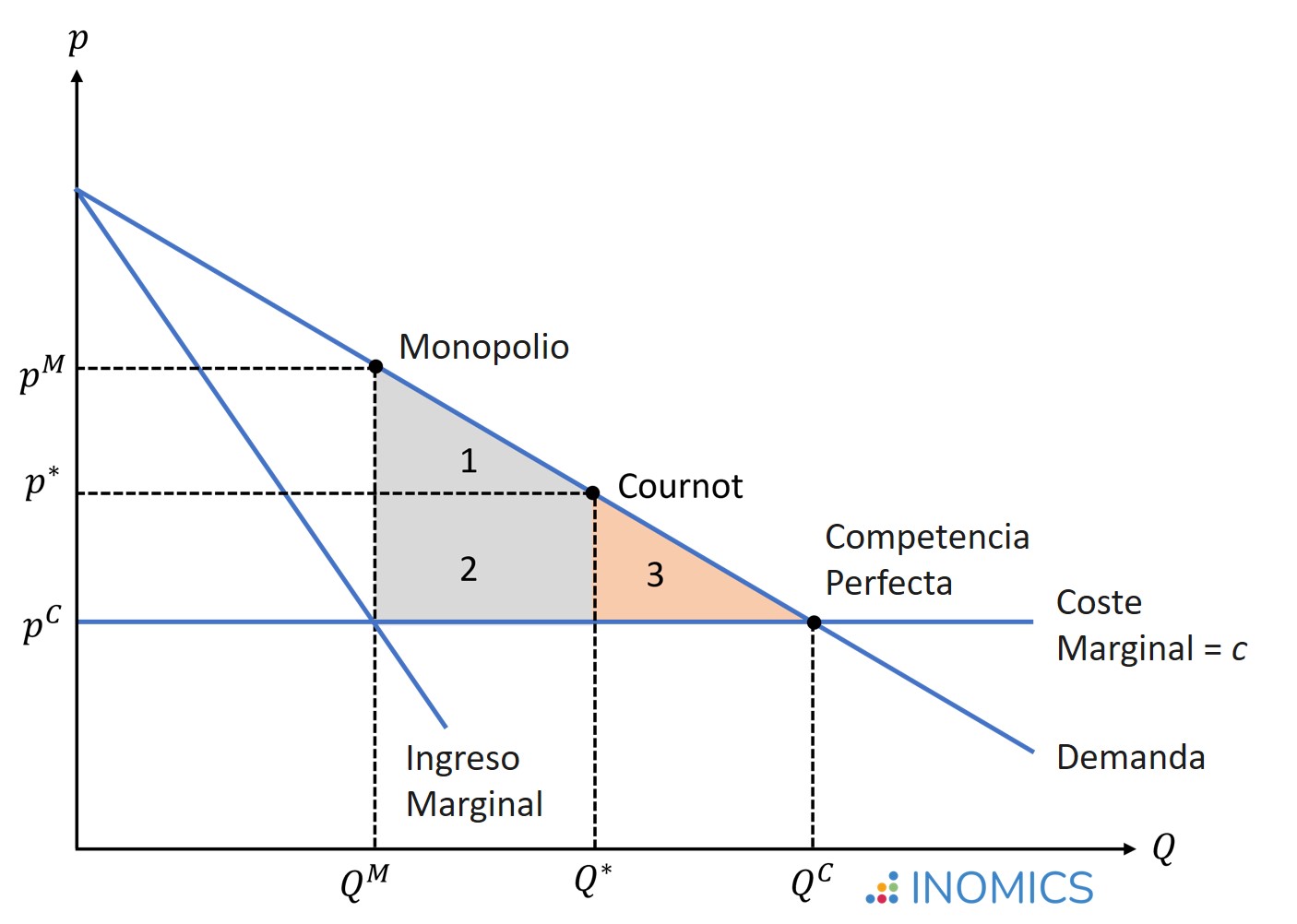
En el gráfico inferior, el cual asume que los costes marginales son constantes para todas las variedades de producción, ilustramos las cantidades y precios de mercado obtenidos en una situación de monopolio, oligopolio de Cournot, y competencia perfecta. El equilibrio de Nash para Cournot se encontrará en un punto entre la solución del monopolio y la de la competencia perfecta.

Las áreas 1 + 2 ilustran el bienestar ganado bajo la competencia de Cournot en comparación con un mercado monopolista, mientras que el área 3 ilustra la pérdida irrecuperable de eficiencia restante en comparación con la competencia perfecta. Antoine Cournot argumentaba que si las dos empresas en el mercado coludían y formaban un cartel, éstas podrían desplazarse hacia la solución del monopolio. Sin embargo, esto no es un equilibrio de Nash estable, dado que ambas empresas considerarían beneficioso desviarse (tal y como la derivación de las funciones de mejor respuesta anteriormente ha mostrado).

La pérdida irrecuperable de eficiencia disminuirá a medida que el número de empresas que compiten en el mercado aumente. Si el número de empresas en el oligopolio de Cournot converge hacia el infinito, el equilibrio de Nash para Cournot convergerá hacia el equilibrio de mercado bajo la competencia perfecta.

Conviene saber

La Organización de Países Exportadores de Petróleo (OPEP) es a menudo mencionada como un buen ejemplo de un oligopolio de Cournot. La investigación ha mostrado que el comportamiento de los países miembros de la OPEP se encuentra en algún lugar entre un oligopolio de Cournot no cooperativo y un cartel. Es decir, mientras haya algo de cooperación, puede ser óptimo, especialmente para los productores más pequeños de la OPEP (cuya producción tiene un menor potencial de impactar sobre los precios de mercado), seguir políticas de producción más expansivas. El estudio realizado por Okullo y Reynès (2016) ofrece algunos conocimientos interesantes al respecto.